Resolviendo el problema de las 3 jarras usando automaton y clpz

El problema de las 3 jarras (Three jugs) consiste en 3 jarras de agua, de 3L, 5L y 8L. Las dos primeras están vacías y la de 8L está llena. El objetivo es que, echando el agua de unas jarras a otras, consigamos tener en alguna jarra 4L exactos. Este problema lo vamos a resolver en Prolog intentando usar una técnica más avanzada de la librería clpz, automaton. Los usos básicos de clpz ya los vimos en otro post.

¿Qué nos ofrece automaton?

Los predicados automaton (automaton/3 y automaton/8) se usan en problemas de scheduling para obtener el orden de las tareas a realizar si estas pueden describirse como un autómata finito determinista (AFD, en inglés las siglas son DFA). Es decir, si describimos el problema como un AFD, podremos pasárselo a clpz para que encuentre la forma más corta de resolver realizar las tareas.

Veamos un ejemplo muy sencillo. Nosotros podemos definir un AFD para analizar la expresión regular "0*1*0*". Es decir, N ceros, seguido de N unos, seguido de N ceros. El diagrama de estados sería el siguiente:

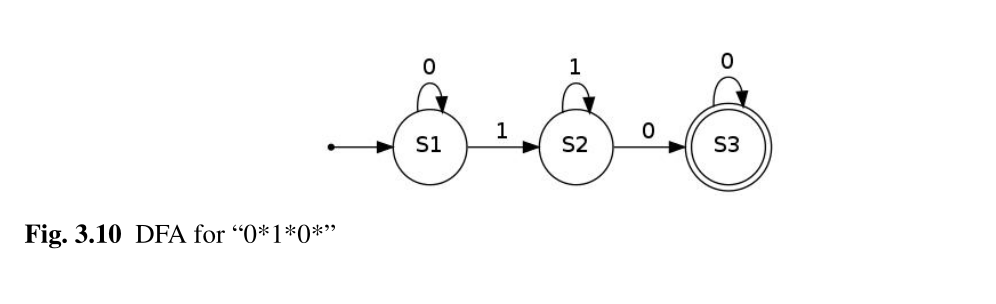
Diagrama sacado del libro Constraint Solving and Planning with Picat

Nosotros empezamos en el estado S1. Si leemos un cero, seguimos en S1. Si leemos un uno, pasamos a S2. En S2 si recibimos un uno seguimos en S2. Si recibimos un cero pasamos a S3. Si recibimos un 1 es un error. Si recibimos un cero, seguimos en S3 hasta acabar.

¿Cómo pasamos esto a automaton? En primer lugar, vamos a usar el predicado automaton/3 que es más sencillo. El otro contiene más opciones y se puede usar en automátas más complejos. El predicado tiene 3 argumentos: lista de entradas, estados especiales (entradas y salidas; source y sink) y finalmente un listado de arcos entre estados tomando una acción. Podemos usarlo para comprobar si una lista cumple el autómata.

?- Vs = [0,0,1,1,1,0], automaton(Vs, [source(s1), sink(s1), sink(s2), sink(s3)], [arc(s1,0,s1), arc(s1,1,s2),arc(s2,1,s2),arc(s2,0,s3),arc(s3,0,s3)]).

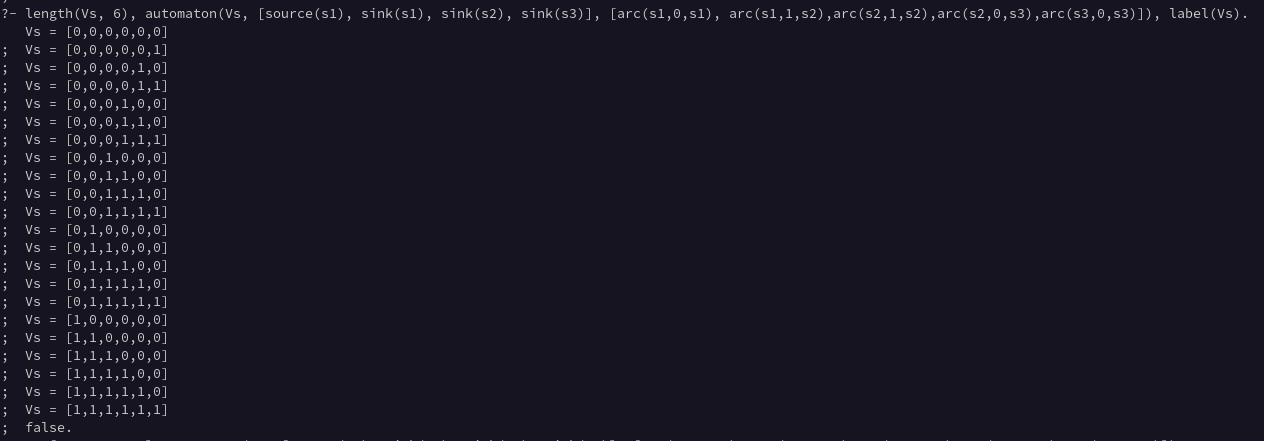
Pero como estamos en Prolog, también podemos preguntar qué listas de longitud N se pueden construir. Para ello necesitamos llamar a label/1, ya que estamos en clpz. Un ejemplo con N=6

?- length(Vs, 6), automaton(Vs, [source(s1), sink(s1), sink(s2), sink(s3)], [arc(s1,0,s1), arc(s1,1,s2),arc(s2,1,s2),arc(s2,0,s3),arc(s3,0,s3)]), label(Vs).

El problema de las 3 jarras

El principal problema de resolver problemas mediante su traslación a DFA, es que muchas veces se requieren muchos pasos para transformar los datos a un DFA correcto.

En este caso lo que voy a hacer es buscar una representación programática del estado. Como son 3 jarras, usaré un guión para separar entre los litros que contiene cada jarra en este momento. Es decir, el término 1-2-5 representará al estado en que la primera jarra tiene 1L, la segunda tiene 2L y la tercera tiene 5L. Con esta representación el estado inicial será 0-0-8 y solo hay uno.

Sacar los estados finales ya es más complicado. Para ello primero voy a generar todos los posibles estados que se pueden hacer con 3 jarras y 8L. De esos filtraré en los que alguna jarra contiene 4L exactos.

states(States) :-
    [A,B,C] ins 0..8,
    A+B+C #= 8,
    findall(A-B-C, label([A,B,C]), States).

end_states(States, EndStates) :-
    findall(sink(S), (
		member(S, States),
		S = A-B-C,
		(A = 4; B = 4; C = 4)
	    ), EndStates).

Ahora toca la parte maś compleja que es definir los arcos. Evidentemente no los vamos a escribir a mano, sino que vamos a hacer reglas. Como tenemos ya todos los estados de 8L, vamos a ir filtrando los arcos que van entre dos estados posibles diferentes con una acción. Las acciones las vamos a numerar del 1 al 6, ya que automaton requiere que estas acciones sean números enteros.

De un estado se puede pasar a otro a través de un arco haciendo una acción si tiene sentido el movimiento de litros que hacemos (llenamos la jarra hasta el tope o hasta que nos quedamos sin agua en el origen). Usamos aritmética de clpz.

arcs(States, Arcs) :-
    findall(arc(S0, Action, S1),(
		member(S0, States),
		member(S1, States),
		S0 \= S1,
		arc(S0, Action, S1)
	    ), Arcs).

% Arcs
% Pour from A to B
arc(A-B-C, 1, X-Y-Z) :-
    Dif #= min(A, 5-B),
    X #= A - Dif,
    Y #= B + Dif,
    Z = C.
% Pour from A to C
arc(A-B-C, 2, X-Y-Z) :-
    Dif #= min(A, 8-C),
    X #= A - Dif,
    Y = B,
    Z #= C + Dif.
% Pour from B to C
arc(A-B-C, 3, X-Y-Z) :-
    Dif #= min(B, 8-C),
    X = A,
    Y #= B - Dif,
    Z #= C + Dif.
% Pour from B to A
arc(A-B-C, 4, X-Y-Z) :-
    Dif #= min(B, 3-A),
    X #= A + Dif,
    Y #= B - Dif,
    Z = C.
% Pour from C to A
arc(A-B-C, 5, X-Y-Z) :-
    Dif #= min(C, 3-A),
    X #= A + Dif,
    Y = B,
    Z #= C - Dif.
% Pour from C to B
arc(A-B-C, 6, X-Y-Z) :-
    Dif #= min(C, 5-B),
    X = A,
    Y #= B + Dif,
    Z #= C - Dif.

¡Ya tenemos todas las piezas! Solo hace falta juntarlas para resolver el problema.

:- use_module(library(lists)).
:- use_module(library(clpz)).

solve(Vs) :-
    states(States),
    end_states(States, EndStates),
    arcs(States, Arcs),
    length(Vs, _),
    automaton(Vs, [source(0-0-8)|EndStates], Arcs),
    label(Vs).

% ?- solve(Vs).
%   Vs = [6,4,2,4,6,4]
%;  Vs = [5,1,5,1,3,1,5]
%;  Vs = [6,4,2,4,6,4,2]
%;  Vs = [5,1,5,1,3,1,5,1]
%;  Vs = [5,1,6,4,2,4,6,4]
%;  Vs = [5,2,6,4,2,4,6,4]
%; ...

La solución más corta parece ser [6,4,2,4,6,4]. Con esto ya tendríamos el problema resuelto, pero es cierto que es complicado de interpretar. Vamos a añadir un predicado para explicar la solución.

print(Xs) :- print(Xs, 0-0-8).
print([], _).
print([X|Xs], S) :-
    arc(S, X, S1),
    S = A-B-C,
    S1 = D-E-F,
    format("Going from (~d,~d,~d) to (~d, ~d, ~d)\n", [A,B,C,D,E,F]),
    print(Xs, S1).

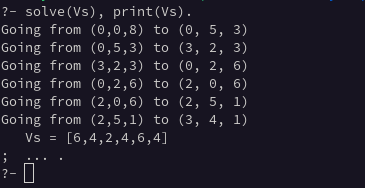
Con esto ya tenemos resuelto el problema de las 3 jarras.