Soccerdoku en Prolog (usando clpz)
No soy especialmente futbolero. Sé las reglas y sé más o menos donde anda cada equipo pero no veo partidos. Sin embargo, con motivo de la Eurocopa 2020 vamos a resolver un problema lógico relacionado con el fútbol, el Soccerdoku. Y lo haremos en Prolog usando la librería clpz
¿Qué es un Soccerdoku?
Un soccerdoku es un problema como el que tenéis arriba (y ese es el que vamos a resolver). Basícamente consiste en rellenar las típicas tablas resumen de los equipos de una liga. Estas tablas tienen varias columnas:
P - Partidos jugados, W = Partidos ganados, L = Partidos perdidos, D = Partidos empatados, GF = goles a favor, GA = goles en contra, Points = Puntos del equipo. Además los equipos están ordenados en la tabla por puntos (de más a menos).
Los puntos se calculan teniendo en cuenta que un partido ganado son 3 puntos para el ganador y cero para el perdedor, y en caso de empate ambos se llevan 1 punto.
La idea es que estas tablas resumen pueden llegar a ser redundantes y ante una tabla incompleta podemos completar el resto de datos.
Modelando el problema - ¿Qué variables?
En este tipo de problemas lo más importante es la elección de lo que van a ser nuestras variables. Normalmente elegiremos lo más fundamental, aquello que nos permita derivar el resto de datos de la tabla. Así pues nuestras variables van a ser el número de goles de cada equipo en cada partido.
Sabemos que son 4 equipos, pero ¿cuántos partidos han jugado? El enunciado nos dice que han jugado todos contra todos una vez, así que han sido 6 partidos. Con esto ya podemos crear las variables, que serán las siguientes:
| Nº Partido | Equipo 1 | Goles equipo 1 | Equipo 2 | Goles equipo 2 |
|---|---|---|---|---|
| 1 | Albion | A1 | United | U1 |
| 2 | Albion | A2 | Town | T2 |
| 3 | Albion | A3 | Rovers | R3 |
| 4 | United | U4 | Town | T4 |
| 5 | United | U5 | Rovers | R5 |
| 6 | Town | T6 | Rovers | R6 |
Nos faltaría una cosa más. ¿Qué valores pueden tener estas variables? El mínimo es 0 (cero goles) ya que no tiene sentido que tomen valores negativos. El máximo es teóricamente infinito pero vemos que ningún equipo tiene más de 4 en Goles a favor (goles que han marcado en todos los partidos, sumados), así que pondremos el máximo a 4.
En Prolog
Voy a usar la librería clpz de Markus Triska. Se puede usar tanto en Scryer Prolog como en SICStus Prolog.
La librería tiene tres partes fundamentales. La primera es la creación de variables, que podemos hacer con ins. Mediante ins creamos las variables, de tipo entero, dentro de un rango. La segunda parte son las restricciones, que añadiremos después, y por último, el etiquetado. El etiquetado es dar un valor concreto a todas las variables en conjunto, de forma que el resultado sea factible. Dicho esto, veamos como se haría:
:- use_module(library(clpz)).
:- use_module(library(format)).
soccerdoku :-
[A1, A2, A3, U4, U5, T6, U1, T2, R3, T4, R5, R6] ins 0..4,
label([A1, A2, A3, U4, U5, T6, U1, T2, R3, T4, R5, R6]),
format("Albion ~d - United ~d~n", [A1, U1]),
format("Albion ~d - Town ~d~n", [A2, T2]),
format("Albion ~d - Rovers ~d~n", [A3, R3]),
format("United ~d - Town ~d~n", [U4, T4]),
format("United ~d - Rovers ~d~n", [U5, R5]),
format("Town ~d - Rovers ~d~n", [T6, R6]).
Como véis, inicializamos todas las variables entre 0 y 4 y después buscamos una solución factible (etiquetado). Como no hay restricciones, el resultado será incorrecto.
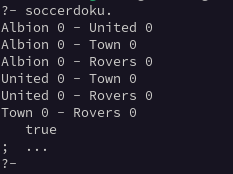
Añadiendo restricciones
Que todos los partidos hayan sido 0 - 0 es incorrecto, pero ¿por qué? Porque tenemos información extra en la tabla original que nos dice que esos resultados no podían ser compatibles. En este problema existen dos tipos de restricciones: las de puntos y las de goles. Vamos con las de goles que son más sencillas.
Los goles a favor tienen que ser la suma de todos los goles que ha marcado un equipo. En la tabla tenemos los goles a favor de todos los equipos. En resumen, podemos decir que A1+A2+A3 debería ser igual a 4. Con clpz podemos expresar esta igualdad mediante el operador #=.
A1 + A2 + A3 #= 4,
U4 + U5 + U1 #= 4,
T6 + T2 + T4 #= 1,
R3 + R5 + R6 #= 1,
De la misma forma podríamos hacerlo con los goles en contra de los que disponemos el dato. En este caso, será la suma de los goles de los oponentes de un equipo en los respectivos partidos. En el caso de United, será A1 + T4 + R5 #= 5.
Con esto hemos acotado las soluciones mucho, pero sigue habiendo más de una solución posible. Vamos a introducir las restricciones de puntos.
Según el enunciado, en un partido el que gana se lleva 3 puntos, el que pierde 0, y si empatan, ambos se llevan 1. Sabemos que Albion tiene 7 puntos y Rovers tiene 1 punto.
Lo primero es hacer un predicado que según los goles de cada partido, nos de los puntos para los equipos participantes. Se puede hacer de la siguiente forma, usando comparadores de clpz:
match_points(Goals1, Goals2, Points1, Points2) :-
Goals1 #> Goals2,
Points1 #= 3,
Points2 #= 0.
match_points(Goals1, Goals2, Points1, Points2) :-
Goals1 #< Goals2,
Points1 #= 0,
Points2 #= 3.
match_points(Goals1, Goals2, Points1, Points2) :-
Goals1 #= Goals2,
Points1 #= 1,
Points2 #= 1.
Y podemos añadir las restricciones de puntos para Albion y Rovers. Con esto ya obtendremos una solución única, que será la correcta.
Código final
El código final es el siguiente:
:- use_module(library(clpz)).
:- use_module(library(format)).
match_points(Goals1, Goals2, Points1, Points2) :-
Goals1 #> Goals2,
Points1 #= 3,
Points2 #= 0.
match_points(Goals1, Goals2, Points1, Points2) :-
Goals1 #< Goals2,
Points1 #= 0,
Points2 #= 3.
match_points(Goals1, Goals2, Points1, Points2) :-
Goals1 #= Goals2,
Points1 #= 1,
Points2 #= 1.
soccerdoku :-
[A1, A2, A3, U4, U5, T6, U1, T2, R3, T4, R5, R6] ins 0..4,
A1 + A2 + A3 #= 4,
U4 + U5 + U1 #= 4,
T6 + T2 + T4 #= 1,
R3 + R5 + R6 #= 1,
A1 + T4 + R5 #= 5,
A2 + U4 + R6 #= 2,
A3 + U5 + T6 #= 3,
match_points(A1, U1, PA1, _),
match_points(A2, T2, PA2, _),
match_points(A3, R3, PA3, PR3),
match_points(U5, R5, _, PR5),
match_points(T6, R6, _, PR6),
PA1 + PA2 + PA3 #= 7,
PR3 + PR5 + PR6 #= 1,
label([A1, A2, A3, U4, U5, T6, U1, T2, R3, T4, R5, R6]),
format("Albion ~d - United ~d~n", [A1, U1]),
format("Albion ~d - Town ~d~n", [A2, T2]),
format("Albion ~d - Rovers ~d~n", [A3, R3]),
format("United ~d - Town ~d~n", [U4, T4]),
format("United ~d - Rovers ~d~n", [U5, R5]),
format("Town ~d - Rovers ~d~n", [T6, R6]).
% sustituye los format con esto para tener la salida alineada y bonita
% Width = 15,
% format("Albion ~t~d~*+ - United ~t~d~*+~n", [A1, Width, U1, Width]),
% format("Albion ~t~d~*+ - Town ~t~d~*+~n", [A2, Width, T2, Width]),
% format("Albion ~t~d~*+ - Rovers ~t~d~*+~n", [A3, Width, R3, Width]),
% format("United ~t~d~*+ - Town ~t~d~*+~n", [U4, Width, T4, Width]),
% format("United ~t~d~*+ - Rovers ~t~d~*+~n", [U5, Width, R5, Width]),
% format("Town ~t~d~*+ - Rovers ~t~d~*+~n", [T6, Width, R6, Width]).
Y el resultado final es:
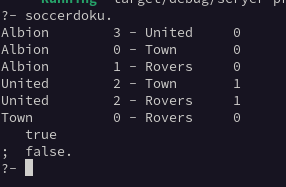
Con esto ya podemos rellenar el resto de la tabla de manera trivial. Albion tuvo dos victorias y un empate, 0 goles en contra. United tuvo 6 puntos, de dos victorias y una derrota. Town tuvo 2 puntos, de dos empates y una derrota. Y Rovers tiene un punto de un emparte y dos derrotas.
¿Qué te parece el soccerdoku? ¿Conocías las capacidades de la librería clpz? Dejadme vuestra opinión en los comentarios. Espero que os haya gustado este pequeño pasatiempo.
