Reinforcement Learning (Aprendizaje por refuerzo): Q-Learning (parte 3)

Ya hemos visto en posts anteriores qué es al aprendizaje por refuerzo y como podemos modelar los problemas de este tipo con un MDP. Ahora veremos varias técnicas para calcular la función valor de cada estado y, con esta información, mejorar la política.

Programación dinámica

El primero de estos métodos se llama programación dinámica. La programación dinámica es una clase de algoritmos muy eficientes que se basan en resolver problemas con dos cualidades: tienen una subestructura óptima y las subestructuras se repiten. Con lo primero nos referimos a que resolver una parte del problema de forma óptima, nos da la parte óptima de esa subparte en el problema grande (o sea, se puede resolver a cachos y luego juntar, que sigue siendo óptimo). En este blog, ya hablé de otro problema que se resolvía con programación dinámica, el problema de la mochila.

Policy Iteration

Una de las formas en las que podemos usar programación dinámica para calcular la función valor es usar Iterative Policy Evaluation. La idea es empezar con un valor todos los estados, y poco a poco irlos refinando hasta que la solución definitiva de acuerdo a la siguiente fórmula, donde k es la iteración.

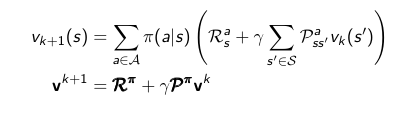
Pongamos el ejemplo del MDP del artículo anterior e intentémos calcular la función valor.

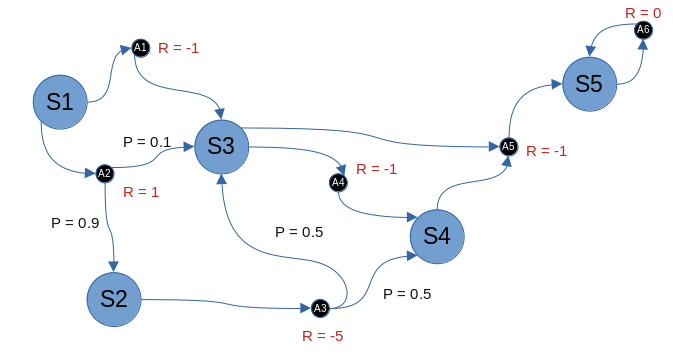
La política que vamos a evaluar es 50/50 aleatoriamente cuando hay posibilidad de elección entre varias acciones. Gamma es 1. Para ello, podemos usar una herramienta como LibreOffice Calc, donde cada fila es un estado, y cada columna es una evaluación k. Las celdas serán el valor de la función valor, que puede depender de la función valor de otros estados en el k inmediatamente anterior.

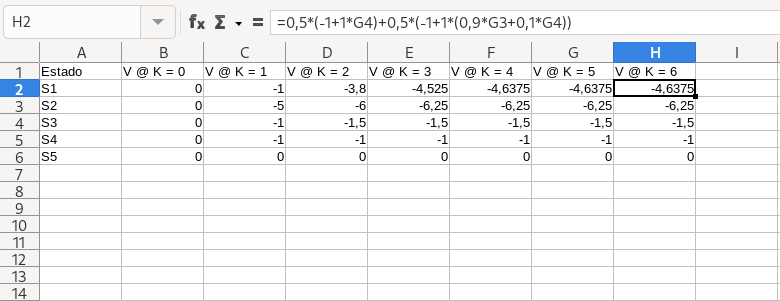
En este caso se puede ver como los valores de la función valor de cada estado se estabilizan a las pocas iteraciones. Ese es el valor correcto de la función valor. Una vez tenemos evaluada la política, podemos mejorarla. ¿Cómo? Actuando de forma egoísta respecto a la función valor, más en concreto la función valor Q, que nos da la función valor de cada acción. Realizando estos dos pasos repetidamente podemos realizar un aprendizaje de política buena. ¿Es la mejor? Puede que sí, pero solo con estos pasos no podemos asegurarlo y tendremos que añadir más

Value Iteration

Otra forma dentro de DP para obtener una buena política es Value Iteration. Aquí no existe una política explícita sino que se actúa de forma greedy sobre las funciones valor que se calculan. La fórmula para la función valor en Value Iteration es ligeramente diferente a la de Policy Iteration.

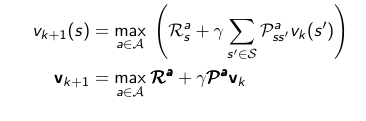
En vez de tomar las acciones en general, se toma siempre la acción de mayor función valor como la que sirva para calcular la función valor de ese estado.

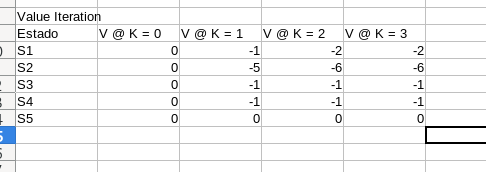
En este ejemplo, los resultados son similares, pero se alcanza la convergencia antes. Este método, a diferencia del anterior, garantiza que la función valor que vamos a obtener es óptima.

Monte Carlo

La programación dinámica tiene técnicas interesantes si conocemos el MDP a priori pero en la mayoría de casos no lo vamos a conocer. Los siguientes métodos, Monte Carlo y Temporal Difference, no usan la estructura del MDP para sus cálculos, simplemente resultados de diferentes ejecuciones.

Monte Carlo se basa en calcular la función valor en base a una media que vamos construyendo poco a poco según vamos realizando ejecuciones. Existen dos tipos: First-Vist and Every-Visit, se diferencian en un pequeño detalle. Vayamos primero con el segundo.

Para evaluar la función valor de un estado, ejecutamos un episodio hasta que acabe. Luego inspeccionamos la historia, cada vez que pasamos por el estado del que estamos calculando el valor, aumentamos el contador N y sumamos el retorno (G) en ese momento. Finalmente dividimos la suma de G entre N y tendremos una aproximación a la función valor para ese estado. Cuando tengamos muchos episodios, la aproximación será más precisa. Si esto solo lo hacemos para la primera vez, tenemos un First-Visit en vez de un Every-Visit.

Temporal Difference

Temporal Difference es muy similar a Monte Carlo, pero con una diferencia fundamental. En vez de usar el retorno real (G), se usa un retorno estimado, basándonos en la recompensa inmediata y la estimación de la función valor del siguiente estado. Esto permite aprender más rápidamente, de secuencias incompletas. Por ejemplo, si vamos en un coche, igual no sabemos si ir por una ruta o por otra es mejor en ese momento (tenemos que esperar al final para saberlo) pero seguro que sabemos que si nos vamos por un barranco vamos a perder mucha recompensa. TD se daría cuenta y en mientras se está ejecutando el episodio, asignaría rápidamente funciones valor bajas a los estados que pensamos que nos llevan al barranco.

Uno de los problemas de TD es que aumenta el bias, aunque reduce la varianza, respecto a Monte Carlo. Por este motivo, si bien TD suele ser más rápido, es mucho más sensible a los valores iniciales de la función valor.

TD tiene diferentes variaciones, dependiendo del número de recompensas reales que vamos a usar en la predicción de G. Si solo usamos la recompensa inmediata, hablaremos de TD(n = 0), si además de esa, usamos una recompensa más del futuro, TD(n = 1), con dos recompensas además de la inmediata, TD(n = 2) y así hasta el infinito. En este caso, no estamos aproximando G, ya que usamos siempre los valores reales. Es por ello que TD(n = infinito) = Monte Carlo.

Sin embargo, como la longitud de los episodios puede ser muy diversa, lo ideal es usar TD(lambda), donde lambda es un valor entre 0 y 1, que ajusta proporcionalmente el número de recompensas que tendremos en cuenta del futuro.

Trazas de elegibilidad

Pongamos el ejemplo de una secuencia donde sonó la campana tres veces, despúes hemos visto una luz y después hemos recibido un shock eléctrico. ¿Qué causó el shock? ¿Fue la luz por ser lo más reciente? ¿O fue la campana, ya que fue más frecuente? ¿Qué debería aprender el agente?

Las trazas de elegibilidad son una medida que nos permite tener en cuenta ambas opciones a la vez. Son usadas en TD(lambda) para calcular los valores reales. No vamos a entrar mucho en detalle de las fórmulas pero si quisiésemos implementar esto en la realidad, las necesitaríamos.

GLIE

Hasta ahora hemos visto como calcular la función valor sin conocer el MDP subyacente de un problema (MonteCarlo y TD), ahora, al igual que con programación dinámica si conocemos el MDP, debemos idear un método para encontrar la política óptima.

Vamos a basarnos en Monte Carlo primeramente y vamos a pensar en hacer una selección greedy sobre la función valor. ¿Es posible? No, porque para ello debemos tener un modelo de MDP. Pero tenemos otra función, la función Q, similar a la función valor pero donde especificamos una acción a tomar. Así pues podemos hacer un algoritmo que evalúe las funciones Q para todas las acciones posibles desde el estado y elegiremos la acción que corresponda a mayor valor de su función Q.

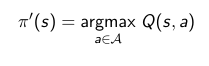
El problema de elegir una acción de forma greedy es que si bien la acción será probablemente buena, seguramente no sea la mejor (recordad, dilema explotación vs exploración del primer post). Es aquí donde entra epsilon-greedy. En esencia es greedy como antes, pero hay una probabilidad no nula de que se elija una acción no mediante el sistema greedy, sino completamente al azar, concretamente la probabilidad es epsilon. Esto mejora las cosas pero no es suficiente todavía para garantizar obtener una solución óptima.

El motivo es que permanentemente vamos a tener una probabilidad de hacer algo aleatorio. Si bien esto nos permite explorar más alternativas, en algún momento será contraproducente. Es por ello que el valor de epsilon debe ir descendiendo progresivamente hasta ser 0. Concretamente podemos decir que epsilon es igual a 1 dividido el número de episodio que estemos procesando. Cuando esto ocurre, tenemos GLIE.

SARSA

Ya tenemos una forma de obtener políticas óptimas basándonos en Monte Carlo. Pero como hemos visto antes, TD(lambda) tiene ciertas ventajas y es más general (Monte Carlo es un caso extremo). Así, pues, ¿qué pasa si usamos la idea de GLIE pero en vez de actualizar Q con G, lo hacemos con la recompensa inmediata y una estimación? Este algoritmo se llama SARSA.

En SARSA también podemos usar lambda, en ese caso deberemos usar trazas de elegibilidad y el pseudocódigo sería algo así:

Q-Learning

Q-Learning es un algoritmo muy similar a SARSA pero con una diferencia clave. Se trata de un algoritmo off-policy. Esto quiere decir que no va a ir siguiendo la propia política que va aprendiendo, sino que va a seguir una política pero va a ir construyendo otra diferente (mejor). En general este tipo de algoritmos son mejores si podemos realizar simulaciones y no nos importa tener más variabilidad durante el entrenamiento.

En Q-Learning la siguiente acción vendrá dada por una política, como por ejemplo, epsilon-greedy, pero a la hora de evaluar el nuevo valor de la función Q, elegiremos la siguiente acción de forma greedy. De este modo, podemos combinar exploración (la política primera explora a veces) pero seguimos construyendo una política óptima.

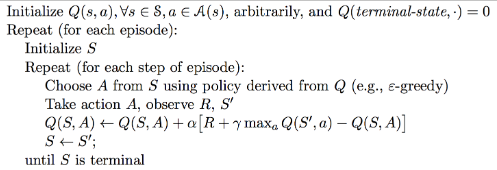
Un ejemplo práctico

He sido muy teórico, y he eso que he resumido muchas cosas. Igual hasta tal punto que no queda muy claro a veces de lo que hablo, si es así, decídmelo y le daré un repaso al apartado. Pero ha llegado el momento de sacar el código. Vamos a implementar Q-Learning para nuestro entorno, ya conocido de otros episodios. Usaremos Python por simpleza, pero lo podéis adaptar fácilmente a cualquier lenguaje.

Lo primero es codificar este entorno en una función, que tomará el estado y la acción y devolverá una recompensa, el siguiente estado y si hemos acabado o no. Las acciones inválidas tienen una recompensa negativa muy fuerte (-10) para que rápidamente el algoritmo no intente hacerlas. Los estados S1, S2, S3, ... se codifican como 0, 1, 2 y las acciones de forma similar. Es decir, se "resta" 1 al número del dibujo. Esto es para que quede más limpio con las operaciones.

import random

def env(state, action):
    if state == 0:
        if action == 0:
            return -1, 2, False
        if action == 1:
            if random.random() < 0.9:
                return -1, 1, False
            else:
                return -1, 2, False
    if state == 1:
        if action == 2:
            if random.random() < 0.5:
                return -5, 2, False
            else:
                return -5, 3, False
    if state == 2:
        if action == 3:
            return -1, 3, False
        if action == 4:
            return -1, 4, True
    if state == 3:
        if action == 4:
            return -1, 4, True
    
    # invalid action
    return -10, state, False

Ahora viene Q-Learning, del pseudocódigo podemos implementar fácilmente el código real. El valor de Q lo vamos a almacenar en una matriz de estados x acciones. Inicializada todoa unos salvo los estados terminales. La política que guía será epsilon-greedy con epsilon igual a 1/k y las constantes gamma y alpha se ajustan a 0.99 y 0.1 respectivamente.

import random
import numpy as np

def qlearn():
    gamma = 0.99
    alpha = 0.1
    q = np.ones((5, 6))
    q[4,:] = 0 # terminal state
    for k in range(1, 1000):
        s = 0
        epsilon = 1/k
        while True:
            if random.random() < epsilon:
                a = random.randint(0, 5)
            else:
                a = np.argmax(q[s,:])
            reward, next_state, done = env(s, a)
            q[s, a] = q[s, a] + alpha*(reward+gamma*np.max(q[next_state, :])-q[s, a])
            s = next_state
            if done:
                break
    return q

Código disponible en GitHub

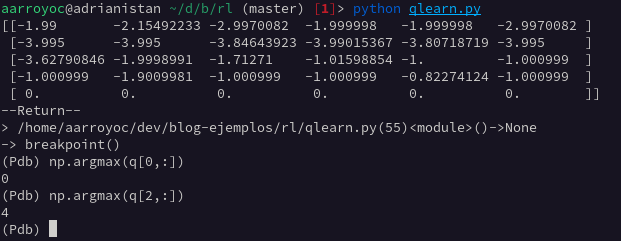
Y ya estaría. Ahora podemos llamar a la función qlearn para obtener la matriz que representa la función Q. Nuestra política será actuar de forma greedy con esta tabla. Veamos un ejemplo.

Si estamos en S1, la política nos manda tomar A1. La cual nos lleva a S3. La política nos manda ahora tomar A5, la cual nos lleva a S5 y finaliza el episodio. Este es el recorrido óptimo. Pero desde otros estados de partida, también nos llevaría a tomar las mejores acciones. Y esto sin saber como funciona la función env, de la que solo ve las salidas dadas las entradas.

Y con esto ya estarían los métodos clásicos de Aprendizaje por Refuerzo. Lo siguiente será comentar las técnicas más modernas. No dejéis de consultar la bibliografía (primer post) si queréis profundizar más.