Reinforcement Learning (Aprendizaje por refuerzo): MDPs y ecuación de Bellman

En el anterior post vimos una introducción a algunos conceptos del aprendizaje por refuerzo. Una cosa que se vio, es que los problemas se pueden modelar como MDP. En este post veremos como se hace, ya que nos permitirá visualizar mejor qué es lo que ocurre dentro de un problema de RL y nos da una base matemática para encontrar soluciones.

¿Qué es un MDP?

Un MDP (Markov Decission Process) es un entorno donde todos los estados son Markov que define las transiciones entre estos, recompensas, ... Los estados Markov como ya vimos, son autoexplicativos, y no necesitamos saber por qué estados ha pasado antes porque el propio hecho de estar en ese estado ya contiene esa información.

Para definir un MDP debemos definir los siguientes elementos:

• Un cojunto finito de estados (S)
• Un conjunto finito de acciones (A)
• Una matriz de transición de estados. Dado un estado actual y una acción, nos dirá la probabilidad de ir a cada uno de los otros estados.
• Una función de recompensa que toma el estado actual y la acción actual.
• Gamma, el factor de descuento, entre 0 y 1.

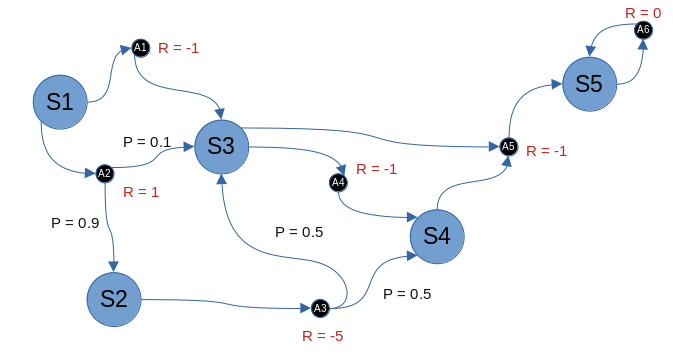
Podemos representar un MDP de forma gráfica tal que así. Este MDP nos servirá de ejemplo

El MDP tiene 5 estados (uno de ellos final). En algunos estados podemos tomar varias acciones, en algunos solo una. Además algunas acciones nos llevan de forma directa a otro estado, mientras que en otras hay una probabilidad de ir a un estado u a otro. Cada acción lleva asociada una recompensa. El objetivo es ir de S1 a S5 con la mayor recompensa posible.

Definimos como retorno, G_t, a la suma de las recompensas descontadas desde el instante de tiempo t. ¿Descontadas? Quiere decir, que cada vez valgan menos, en base al valor gamma. El valor gamma sirve para controlar entre la recompensa inmediata y la recompensa futura. Un valor de gamma igual a cero hace que el agente sea miope y analice más allá del primer paso. Un valor de gamma igual a uno hace que el agente tenga en cuenta todo sin priorizar por tiempo. En general, el mejor valor no será ninguno de los dos extremos (0 o 1) sino un valor intermedio.

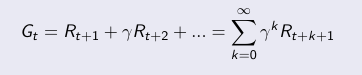
Una vez tengamos un MDP, podemos asignarle una política. La política nos dice para cada estado, qué acción hay que tomar, con una cierta probabilidad. Cada ejecución de la política sobre el MDP se le llama episodio.

Con un MDP y una política podemos definir su función valor V, para un estado s. Se define como la media de los retornos desde el estado actual.

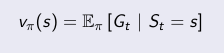
También podemos definir la función Q, se define como la media de los retornos desde el estado actual tomando la acción a.

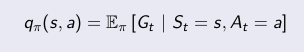
Ecuación de Bellman

La forma anterior que hemos visto de expresar la función valor es matemáticamente correcta pero poco práctica. Realizando unas transformaciones podemos convertirla en la ecuación de Bellman.

De forma matricial:

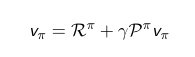
De forma individual:

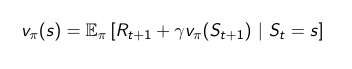
La ecuación de Bellman es interesante, porque es resoluble, aunque algorítmicamente no es muy interesante. En la práctica solo podemos resolver pequeños MDP. Pero es la base paa

Calculemos los valores de la función valor para algunos estados del MDP de la imagen (asumiremos gamma = 1 y una política 100% aleatoria). El más sencillo es S5. Como la única posibilidad es tomar A6, que nos devuelve a S5 y tiene recompensa 0, v(S5) = 0. Para S4, es también sencillo, ya sabiendo como funciona S5. En este caso solo hay una opción que es tomar A5. Entonces v(S4) = -1 + 1*v(S5) = -1. Ahora pensemos la función valor de S3. Sería v(S3) = 0,5*(-1 + 1*v(S5)) + 0,5*(-1 + 1*v(S4)) = -0,5 - 1 = -1,5 y así sucesivamente.

Se define una función valor óptima para aquella que consigue el valor más elevado, sobre todas las políticas existentes. Al obtener una función valor óptima resolvemos el MDP y sabemos el rendimiento óptimo que podemos lograr.

Resolver este problema no es fácil y no existe una solución genérica. Existen diferentes métodos iterativos que tratan de encontrar esa política que consiga la función valor óptima. Algunos de ellos son: Value Iteration, Policy Iteration, Q-learning y SARSA. Y los veremos en el siguiente post.