Paralelismo para lelos
No podía hablar de paralelismo sin hacer el chiste del título. En estos artículos sobre paralelismo hablaremos sobre por qué es algo esencial en la programación en 2025 y las diferentes formas de alcanzarlo: SIMD, multicore, sistemas distribuidos y GPUs.
¿Por qué necesitamos paralelismo?
Históricamente, el funcionamiento de un ordenador, en concreto de la CPU, la parte más importante, ha sido secuencial. La CPU iba leyendo instrucciones e iba ejecutándolas una detrás de otra. El ritmo lo marca la frecuencia del procesador, medido en herzios. Estas operaciones manipulan datos en memoria, una memoria global, sobreescribible y de acceso rápido pero volátil. Muchos lenguajes de programación como C, Java o Python se basan en esa idea de ir haciendo operaciones una detrásde otra (el paradigma imperativo).
Las CPUs de los 80 funcionaban así. Pero queremos más rendimiento. La opción sencilla es elevar la frecuencia de la CPU. Durante un tiempo esto fue fácil, aprovechando la ley de Moore, podíamos tener transistores más pequeños, que gastan menos energía y podemos aumentar la frecuencia sin aumentar el calor generado. Ya en los 90 se llegó prácticamente al límite, se tuvo que empezar a refrigerar las CPUs de forma activa, con ventiladores o con sistemas líquidos.
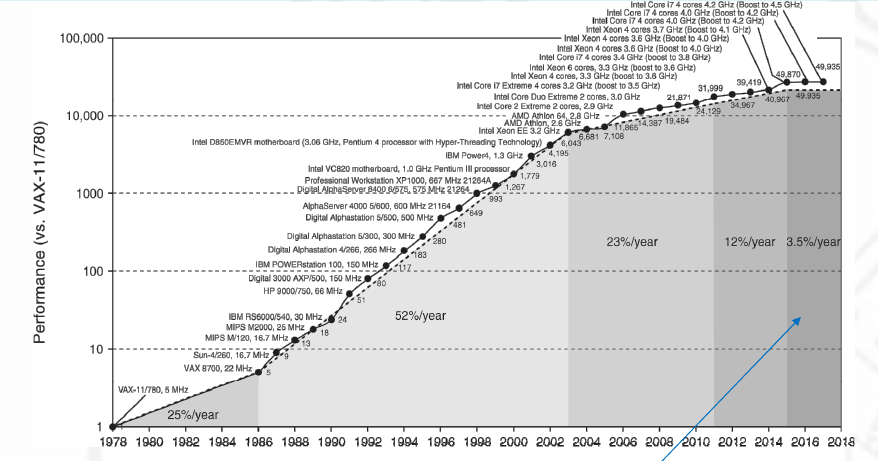
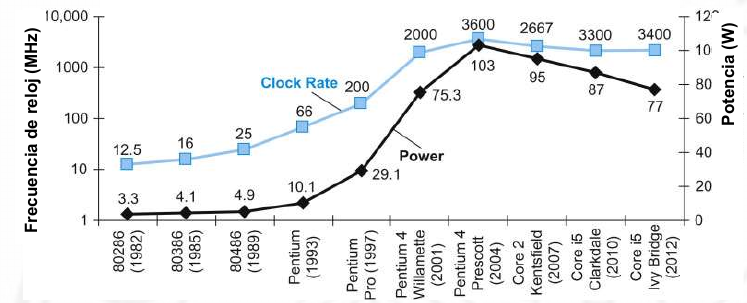
A este problema se le llama el del muro de potencia, y es que básicamente miniaturizar y bajar voltajes te permite subir frecuencias manteniendo un nivel de potencia energética similar pero hay límites físicos.
Ante esta tesitura hay varias opciones. La primera, que no vamos a ver en detalle ya que la hace la CPU sin que nos demos cuenta es, aprovechando la ley de Moore, hacer CPUs más complejas con pipelines y sistemas de predicción. Es decir, el código ejecuta varias instrucciones a la vez, en diferentes fases. Incluido tomar los saltos antes de que se sepa qué va a salir (hace los ifs antes de saber si se va a ejecutar la parte del true o la del false). Pero todo esto de forma interna sin que el programa note la diferencia con una CPU que no haga esto. Esto funciona bastante bien, aunque en código nativo se nota más la diferencia (la CPU ve mejor los patrones para hacer predicciones).
Otra opción es fijarse en qué otras cosas ralentizan la ejecución. Un tema muy importante es el acceso a memoria, que a las frecuencias actuales es muy lento comparado con hacer cosas en la CPU (varios órdenes de magnitud, piensa 100, 1000 veces más lento). Si una instrucción que necesita datos en memoria la conseguimos acelerar, tendremos mucho impacto. Esto se soluciona con memorias caché en la CPU, cada vez más grandes. Esto tiene grandes beneficios pero los lenguajes que usan estructuras de datos tipo Array son los que más, ya que normalmente las cachés se traen áreas de memoria de golpe y en los arrays, todo esta almacenado junto (a diferencia de las listas enlazadas).
No obstante, ahora vamos a centrarnos en aquellas mejoras que necesitan de que el programador las use. Y para ello vamos a poner un problema práctico.
El fractal de Mandelbrot
El fractal de Mandelbrot es un fractal comúnmente usado para mostrar paralelismo ya que sus cálculos se pueden dividir de forma muy sencilla. En la realidad hay problemas donde es más difícil encontrar la paralelización, si es que se puede (nueve mujeres no dan un bebe en un mes) o incluso puede que haya que usar algoritmos a priori menos eficientes para acceder a ella.
El fractal se define en el plano de los números imaginarios. Por cada punto c, se ejecuta iterativamente la siguiente función.
Consideramos que si tras N iteraciones, el valor se escapa (su valor absoluto es 2 o más) entonces forma parte del conjunto. A más iteraciones obtendremos imágenes más precisas.
Por comodidad podemos acotar el plano imaginario a (-2.5, 1.0) en la dimensión real y a (-1, 1) en la dimensión imaginaria.
Una primera versión que se nos puede ocurrir sin tener en cuenta el rendimiento es esta:
use image::RgbImage;
use std::path::Path;
use std::time::Instant;
const ITERATIONS: u32 = 100;
const WIDTH: u32 = 3500;
const HEIGHT: u32 = 2000;
const BUFFER_SIZE: usize = (WIDTH * HEIGHT * 3) as usize;
struct Complex {
real: f64,
im: f64,
}
impl Complex {
fn square(&mut self) {
let prev_real = self.real;
self.real = self.real * self.real - self.im * self.im;
self.im = 2.0 * prev_real * self.im;
}
fn plus(&mut self, other: &Complex) {
self.real = self.real + other.real;
self.im = self.im + other.im;
}
fn abs(&self) -> f64 {
(self.real * self.real + self.im * self.im).sqrt()
}
}
fn main() {
// sequential
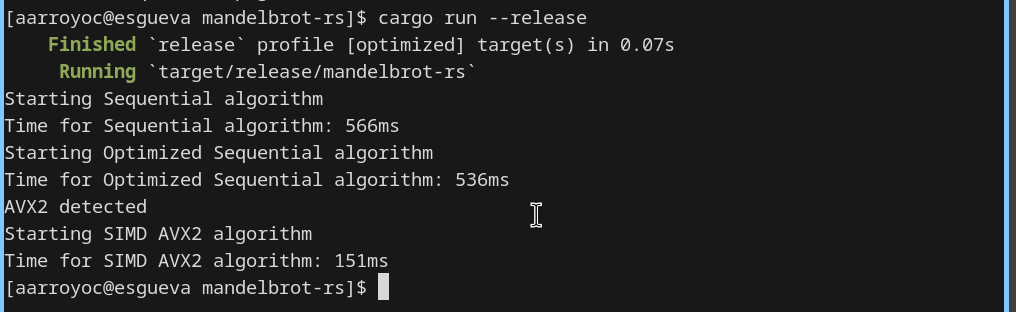
println!("Starting Sequential algorithm");
let mut buffer: Vec<u8> = vec![0; BUFFER_SIZE];
let now = Instant::now();
for x in 0..WIDTH {
for y in 0..HEIGHT {
let c = Complex {
real: x as f64 / 1000.0 - 2.5,
im: y as f64 / 1000.0 - 1.0,
};
let mut z = Complex {
real: 0.0,
im: 0.0,
};
let mut i = 0;
while i < ITERATIONS && z.abs() < 2.0 {
z.square();
z.plus(&c);
i = i + 1;
}
if i == ITERATIONS {
let index = ((y * WIDTH + x) * 3) as usize;
buffer[index] = 255;
buffer[index+1] = 255;
buffer[index+2] = 255;
}
}
}
let elapsed = now.elapsed();
println!("Time for Sequential algorithm: {}ms", elapsed.as_millis());
save_fractal(buffer, &Path::new("sequential.png"));
}
fn save_fractal(buffer: Vec<u8>, path: &Path) {
let img = RgbImage::from_raw(WIDTH, HEIGHT, buffer).unwrap();
img.save(path).unwrap();
}
Es un algoritmo que va rellenando un buffer de imagen con el resultado de las iteraciones. La salida es la que se puede ver en la imagen de abajo. En mi ordenador tarda aproximadamente 570ms.

SIMD
La primera solución para mejorar el rendimiento en CPUs modernas es tambiién la menos conocida. Se trata de usar las instrucciones SIMD o vectoriales. Estas instrucciones se añadieron a x86 a finales de los 90 y básicamente nos permite hacer la misma operación, con datos diferentes, a la vez.
Pongamos un ejemplo: en ensamblador, si queremos hacer una suma, tendremos los sumandos en un registro cada uno, de 64 bits. Y el resultado de la suma se almacena en uno de esos registros o en otro. Ya hemos dicho que hay trucos a nivel de CPU para hacer varias cosas a la vez pero tienen limitaciones porque tienen que, de puertas para fuera, seguir siendo secuenciales.
Ahora imaginemos que tenemos que hacer cuatro sumas seguidas, independientes entre sí. Pues podemos poner los cuatro "adds" uno detrás de otro. O podemos decirle a la CPU que haga las 4 sumas a la vez, un una misma instrucción. Para ello, cargamos los sumandos de un lado en registros de 256 bits y los otros en otro registro de 256 bits. Luego hacemos la suma.
Esta forma de trabajar se pensó originalmente para tareas multimedia donde es relativamente fácil encontrarse con datos en vectores que requieren un procesamiento para todos igual y sin dependencias entre sí. Arquitecturas como la de la PS2 también se basaban en CPUs con instrucciones para ir en paralelo así como registros de un tamaño muy grande para poder empaquetar estosdatos, en su caso registros de 128 bits, en CPUs modernas x84-64 tenemos AVX10 con registros de 512 bits. Sin embargo para algunas tareas mucho trabajo se ha movido a las GPUs, similares pero diferentes. Las veremos más adelante.
if is_x86_feature_detected!("avx2") {
println!("AVX2 detected");
println!("Starting SIMD AVX2 algorithm");
let mut buffer: Vec = vec![0; BUFFER_SIZE];
let now = Instant::now();
unsafe {
let zeros = _mm256_set1_pd(0.0);
let two = _mm256_set1_pd(2.0);
let four = _mm256_set1_pd(4.0);
let ones = _mm256_set1_pd(1.0);
for x in 0..WIDTH {
let mut y = 0;
while y < HEIGHT {
let mut xs = _mm256_set1_pd(x as f64);
let mut ys = _mm256_set1_pd(y as f64);
let mut a = _mm256_set_pd(0.0, 1.0, 2.0, 3.0);
ys = _mm256_add_pd(ys, a);
a = _mm256_set1_pd(1000.0);
xs = _mm256_div_pd(xs, a);
ys = _mm256_div_pd(ys, a);
a = _mm256_set1_pd(2.5);
let cxs = _mm256_sub_pd(xs, a);
let cys = _mm256_sub_pd(ys, ones);
let mut zxs = zeros;
let mut zys = zeros;
let mut cmp = ones;
for _ in 0..ITERATIONS {
let zx_square = _mm256_mul_pd(zxs, zxs);
let zy_square = _mm256_mul_pd(zys, zys);
let abs = _mm256_add_pd(zx_square, zy_square);
cmp = _mm256_cmp_pd(abs, four, 1);
if _mm256_testz_pd(cmp, cmp) == 1 {
break;
}
let previous_zxs = zxs;
zxs = _mm256_sub_pd(zx_square, zy_square);
zxs = _mm256_add_pd(zxs, cxs);
zys = _mm256_mul_pd(two, zys);
zys = _mm256_mul_pd(zys, previous_zxs);
zys = _mm256_sub_pd(zys, cys);
}
let (cmp3, cmp2, cmp1, cmp0): (f64, f64, f64, f64) = std::mem::transmute(cmp);
if cmp3 != 0.0 {
let index = (((y + 3) * WIDTH + x) * 3) as usize;
buffer[index] = 255;
buffer[index+1] = 255;
buffer[index+2] = 255;
}
if cmp2 != 0.0 {
let index = (((y + 2) * WIDTH + x) * 3) as usize;
buffer[index] = 255;
buffer[index+1] = 255;
buffer[index+2] = 255;
}
if cmp1 != 0.0 {
let index = (((y + 1) * WIDTH + x) * 3) as usize;
buffer[index] = 255;
buffer[index+1] = 255;
buffer[index+2] = 255;
}
if cmp0 != 0.0 {
let index = ((y * WIDTH + x) * 3) as usize;
buffer[index] = 255;
buffer[index+1] = 255;
buffer[index+2] = 255;
}
y = y + 4;
}
}
}
La manera de usar estas instrucciones de ensamblador en lenguajes como Rust es mediante intrinsics, que son funciones que por debajo llaman a la instrucción de ensamblador concreta pero añadiendo información útil al compilador.
En este caso concreto uso AVX2, que tiene registros de 256 bits. Los intrinsics como _mm256_set_pd nos permiten cargar 4 double/f64 en uno de estos registros. _mm256_set1_pd replica el número en los 4 huecos. Como veis la idea para acelerar esto es hacer las mismas operaciones pero de 4 en 4, por eso el bucle de y avanza de 4 en 4. En este caso como HEIGHT es múltiplo de 4 no tendremos ningún dato suelto.
Vamos haciendo las sumas, restas, multiplicaciones y divisiones en paralelo para los 4. ¿Pero que pasa cuando uno cumple con la condición de parar? No podemos parar porque entonces pararíamos los 4, cuando solo uno podía parar. Pero si no paramos nunca, vamos a hacer muchas operaciones de más. En este caso el problema tiene solución fácil, ya que podemos seguir haciendo cuentas con uno que ya se ha salido y no va a volver a entrar. Así pues podemos comprobar todos a la vez también (cmp existe en AVX2) y podemos comprobar si todos cumplen. En este caso cuando los 4 se pasen, cortamos el bucle. Si no se sigue hasta el final de las iteraciones.
Finalmente podemos leer el resultado de nuestros registros de 256 bits, con transmute y observando que x86-64 es Little Endian. Podemos sacar los resultados y escribiendo en el buffer de imagen los colores.
El resultado es magnífico, prácticamente reducimos por 4 el tiempo necesario, obteniendo ahora 150ms. A cambio el código se ha vuelto muy ilegible ya que es una especie de pseudo ensamblador. Los lenguajes como C o Rust intentan autovectorizar y usar estas instrucciones sin que nos demos cuenta para evitar tener que escribir este código feo pero no son capaces de hacerlo en código medianamente complejo.