Optimizar una mudanza (o un proyecto de software) en Prolog
Seguimos viendo aplicaciones puzzles en Prolog, ayudándonos de clpz y hoy nos toca uno con multitud de aplicaciones prácticas. El problema de la mudanza consiste en que hay que mover unas piezas de mobiliario (tareas). Algunas de estas necesitan varias personas para poder moverse y se tarda un tiempo en moverlas. Además, hay algunos muebles que tienen que moverse antes que otros debido a su disposición en la casa. Si sois 4 amigos, ¿cuál es el tiempo mínimo que podéis tardar en mover todo?

A continuación, veamos una tabla detallada con los objetos a mover, el número de personas que se necesitan, cuánto se tarda y si hay alguna restricción adicional.
| Mueble | Personas | Tiempo | Notas |
|---|---|---|---|
| Piano | 3 | 30 | |
| Cama | 3 | 20 | Tiene que moverse antes que el piano |
| Mesa | 2 | 15 | |
| TV | 2 | 15 | Tiene que moverse antes que la mesa |
| Silla 1 | 1 | 10 | |
| Silla 2 | 1 | 10 | |
| Silla 3 | 1 | 10 | |
| Silla 4 | 1 | 10 | |
| Estantería 1 | 2 | 15 | Tiene que moverse antes que la cama |
| Estantería 2 | 2 | 15 | Tiene que moverse antes que la mesa |
Podemos empezar viendo cuáles van a ser las variables de nuestro problema. En este tipo de problemas, una buena selección de variables suele ser el tiempo de inicio y el de finalización de cada tarea. El dominio de esta variable la podemos poner entre 0 (tiempo de inicio de la mudanza) y el resultado de sumar todos los tiempos. Ese sería el peor caso, donde todas las tareas se tendrían que hacer de forma secuencial.
Para realizar una asignación de tareas con un recurso finito (en este caso las personas), de modo que las tareas puedan hacerse sin cortes y en ningún instante de tiempo haya más uso de recursos que el límite, clpz nos ofrece una constraint específica llamada cumulative/2. A esta constraint se le debe pasar una lista de tareas, así como el límite de recursos finitos.
moving(Vars) :-
Vars = [StartPiano, EndPiano, StartBed, EndBed, StartTable, EndTable, StartTV, EndTV,
StartChair1, StartChair2, StartChair3, StartChair4, EndChair1, EndChair2, EndChair3, EndChair4,
StartShelf1, StartShelf2, EndShelf1, EndShelf2],
Vars ins 0..150,
% Tasks
Tasks = [
task(StartPiano, 30, EndPiano, 3, _),
task(StartBed, 20, EndBed, 3, _),
task(StartTable, 15, EndTable, 2, _),
task(StartTV, 15, EndTV, 2, _),
task(StartChair1, 10, EndChair1, 1, _),
task(StartChair2, 10, EndChair2, 1, _),
task(StartChair3, 10, EndChair3, 1, _),
task(StartChair4, 10, EndChair4, 1, _),
task(StartShelf1, 15, EndShelf1, 2, _),
task(StartShelf2, 15, EndShelf2, 2, _)
],
% Cumulative constraint
cumulative(Tasks, [limit(4)]).
No obstante, esto solo nos da una asignación de las tareas sin tener en cuenta las restricciones de dependencia. Afortunadamente, las podemos expresar como restricciones normales de clpz, ya que tenemos los tiempos. Lógicamente, si la TV tiene que moverse antes que la mesa, entonces el tiempo de finalización de la tarea de la TV debe ser menor que el tiempo de inicio de la mesa.
% Must be moved before
EndBed #< StartPiano,
EndTV #< StartTable,
EndShelf1 #< StartBed,
EndShelf2 #< StartTable,
Con esto tendríamos una asignación válida, pero no óptima. Para conseguir un resultado óptimo deberemos minimizar sobre el máximo de los tiempos de finalización. Para ello, calculamos con un predicado recursivo el tiempo de finalización máximo y esa variable se la pasamos a labeling/2 con el objetivo de minimizar. El resultado final es el siguiente:
:- use_module(library(clpz)).
moving(Vars, EndTime) :-
Vars = [StartPiano, EndPiano, StartBed, EndBed, StartTable, EndTable, StartTV, EndTV,
StartChair1, StartChair2, StartChair3, StartChair4, EndChair1, EndChair2, EndChair3, EndChair4,
StartShelf1, StartShelf2, EndShelf1, EndShelf2],
Vars ins 0..100,
% Tasks
Tasks = [
task(StartPiano, 30, EndPiano, 3, _),
task(StartBed, 20, EndBed, 3, _),
task(StartTable, 15, EndTable, 2, _),
task(StartTV, 15, EndTV, 2, _),
task(StartChair1, 10, EndChair1, 1, _),
task(StartChair2, 10, EndChair2, 1, _),
task(StartChair3, 10, EndChair3, 1, _),
task(StartChair4, 10, EndChair4, 1, _),
task(StartShelf1, 15, EndShelf1, 2, _),
task(StartShelf2, 15, EndShelf2, 2, _)
],
% Must be moved before
EndBed #< StartPiano,
EndTV #< StartTable,
EndShelf1 #< StartBed,
EndShelf2 #< StartTable,
% EndTime
end_time(EndTime, [EndPiano, EndBed, EndTable, EndTV, EndChair1, EndChair2, EndChair3, EndChair4, EndShelf1, EndShelf2]),
% Cumulative constraint
cumulative(Tasks, [limit(4)]),
% Find solution
labeling([ff, min(EndTime)], Vars).
end_time(EndTime, [EndTime]).
end_time(EndTime, [X|Xs]) :-
end_time(EndTime0, Xs),
EndTime #= max(X, EndTime0).
run :-
moving([StartPiano, EndPiano, StartBed, EndBed, StartTable, EndTable, StartTV, EndTV,
StartChair1, StartChair2, StartChair3, StartChair4, EndChair1, EndChair2, EndChair3, EndChair4,
StartShelf1, StartShelf2, EndShelf1, EndShelf2], EndTime),
format("Optimal time: ~d~n", [EndTime]),
format("Piano ~d ~d~n",[StartPiano, EndPiano]),
format("Bed ~d ~d~n",[StartBed, EndBed]),
format("Table ~d ~d~n",[StartTable, EndTable]),
format("TV ~d ~d~n",[StartTV, EndTV]),
format("Chair 1 ~d ~d~n",[StartChair1, EndChair1]),
format("Chair 2 ~d ~d~n",[StartChair2, EndChair2]),
format("Chair 3 ~d ~d~n",[StartChair3, EndChair3]),
format("Chair 4 ~d ~d~n",[StartChair4, EndChair4]),
format("Shelf 1 ~d ~d~n",[StartShelf1, EndShelf1]),
format("Shelf 2 ~d ~d~n",[StartShelf2, EndShelf2]).
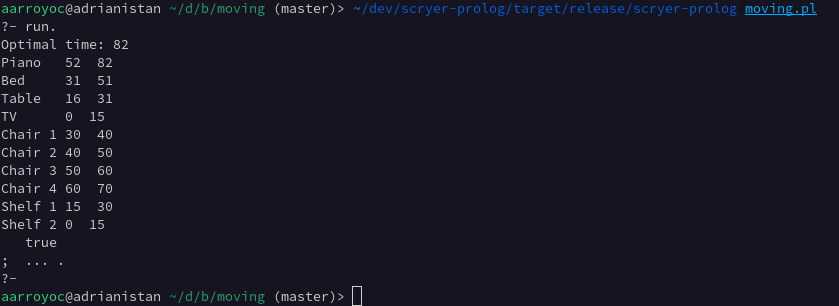
¡Con esto podemos hacer la mudanza de forma óptima! Y quién dice mudanza, dice la planificación de un proyecto de software por ejemplo. La constraint cumulative es verdaderamente potente.