Algoritmos genéticos: un caso práctico
Existen muchos tipos de algoritmos. Hoy vamos a hablar de un tipo de algoritmo no demasiado conocido, los algoritmos genéticos, que son de la familia de los algoritmos evolutivos. Además veremos su aplicación práctica en el vectorizado de imágenes con un programa que he realizado en Rust.
¿Qué es un algoritmo genético?
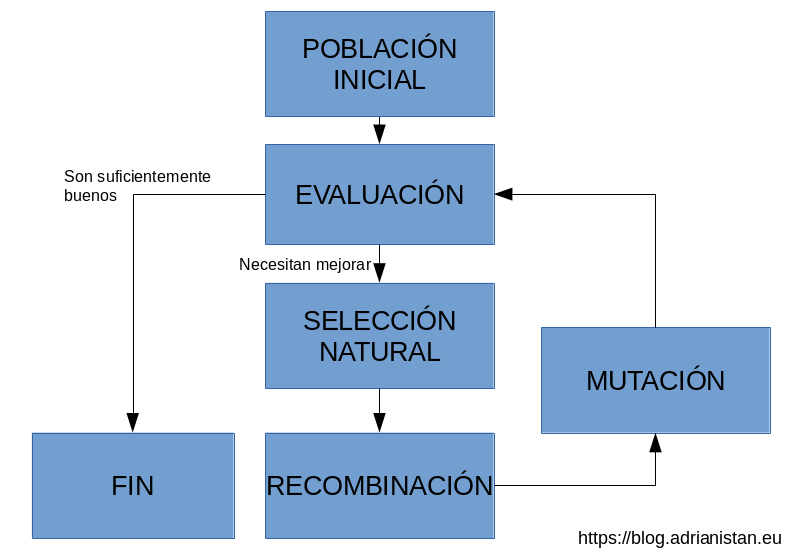
Un algoritmo genético es un algoritmo inspirado en el mecanismo de la naturaleza de la evolución biológica, descrita por Darwin allá por 1859 en el libro El Origen de las Especies. La idea es tener un conjunto de individuos (posibles soluciones). Estos individuos son evaluados para ver qué tan buenos son. Quedarnos con los mejores y proceder a la creación de nuevos individuos como resultados de la recombinación genética de dos individuos (como en la reproducción sexual). Posteriormente añadir alguna mutación genética para explorar nuevas posibilidades ligeramente diferentes. Proceder de nuevo a la selección natural hasta que tengamos individuos lo suficientemente buenos para nosotros.
Normalmente no son los algoritmos más eficientes ni tienen por qué dar un resultado óptimo, pero pueden servir para dar aproximaciones bastante buenas al resultado óptimo. Existen estrategias para mejorar los algoritmos genéticos como la gestión de la antigüedad de los individuos, para evitar máximos locales; la conservación de individuos con mal desempeño, para conservar mayor variedad genética; ...
Como veremos más adelante, uno de los elementos más importante de estos algoritmos es la función de evaluación, que muchas veces es más complicada de programar de lo que parece.
Un caso práctico: vectorizado de imágenes
Para ver como estos conceptos teóricos funcionan en la práctica, vamos a hacer un programa que vectorice imágenes. ¿Esto qué es? Digamos que hay dos tipos de imágenes en informática. Por un lado tenemos las imágenes que almacenan los colores en píxeles (rasterizadas) y por otro lado aquellas que almacenan la imagen como fórmulas matemáticas, que se aplican cuando se quiere ver la imagen (vectoriales). Los formatos más comunes de imágenes rasterizadas son JPEG, PNG, GIF y WEBP. Los formatos más comunes de imágenes vectoriales son SVG y AI.

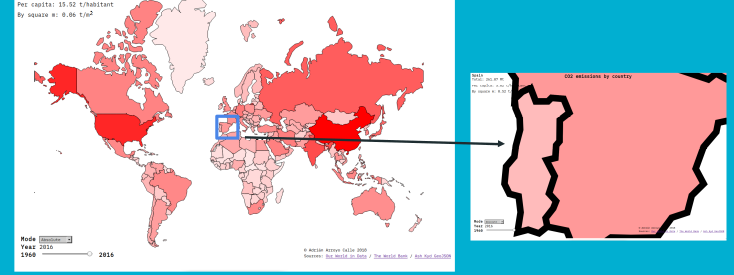
Pasar de una imagen vectorial a una rasterizada es trivial, pero el proceso inverso no lo es, y es justo donde vamos a aplicar el algoritmo genético.
En nuestro caso, vamos a tomar siluetas, negras sobre fondo blanco y tratar de vectorizarlas con curvas de Bézier.
Curvas de Bézier
En los años 60, Pierre Bézier, que trabajaba para Renault, diseñó un tipo de curva para el diseño asistido por ordenador (CAD). Estas son las conocidas como curvas de Bézier. Nuestro algoritmo tratará de encontrar la curva de Bézier más similar a la curva de la imagen rasterizada. Para ello necesitamos un punto de inicio, un punto final y dos puntos de control.
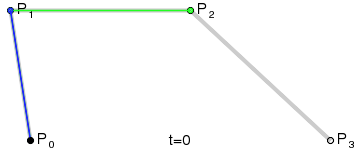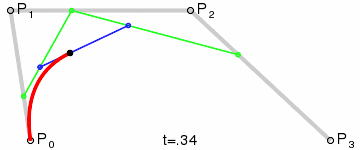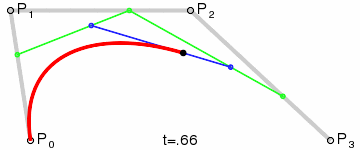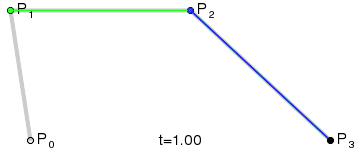
En nuestro algoritmo, las curvas serán los individuos, y las coordenadas de los puntos de control serán los genes (habrá 4 genes por tanto).
Este es el código que he usado para definir las curvas de Bézier en Rust.
#[derive(Copy, Clone)]
pub struct Point {
pub x: f64,
pub y: f64,
}
impl Point {
pub fn distance(&self, other: &Point) -> f64 {
((self.x - other.x).powf(2.0) + (self.y - other.y).powf(2.0)).sqrt()
}
pub fn middle(&self, other: &Point) -> Point {
Point {
x: (self.x + other.x) / 2.0,
y: (self.y + other.y) / 2.0,
}
}
}
#[derive(Clone)]
pub struct Bezier {
pub start: Point,
pub control1: Point,
pub control2: Point,
pub end: Point,
}
impl<'a> Bezier {
pub fn iter(&self) -> BezierIter {
BezierIter {
bezier: self,
position: 0.0,
}
}
}
pub struct BezierIter<'a> {
bezier: &'a Bezier,
position: f64,
}
impl<'a> Iterator for BezierIter<'a> {
type Item = Point;
fn next(&mut self) -> Option {
if self.position > 1.0 {
return None;
}
let x = self.bezier.start.x * (1.0 - self.position).powf(3.0)
+ 3.0 * self.bezier.control1.x * self.position * (1.0 - self.position).powf(2.0)
+ 3.0 * self.bezier.control2.x * self.position.powf(2.0) * (1.0 - self.position)
+ self.bezier.end.x * self.position.powf(3.0);
let y = self.bezier.start.y * (1.0 - self.position).powf(3.0)
+ 3.0 * self.bezier.control1.y * self.position * (1.0 - self.position).powf(2.0)
+ 3.0 * self.bezier.control2.y * self.position.powf(2.0) * (1.0 - self.position)
+ self.bezier.end.y * self.position.powf(3.0);
self.position += 0.01;
Some(Point { x, y })
}}
Encontrar puntos iniciales
El primer paso de nuestro algoritmo es buscar los puntos iniciales (y finales) de las curvas. En definitiva esto es un problema de búsqueda de esquinas.
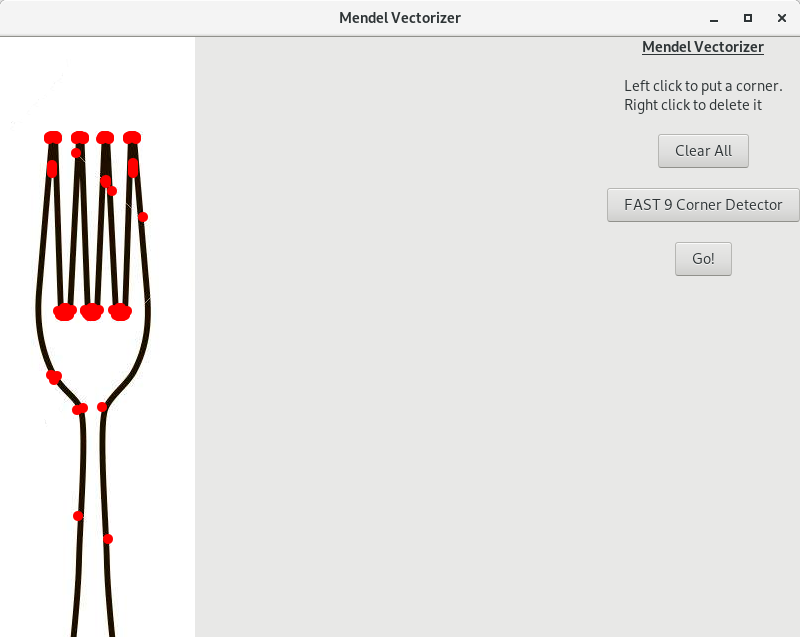
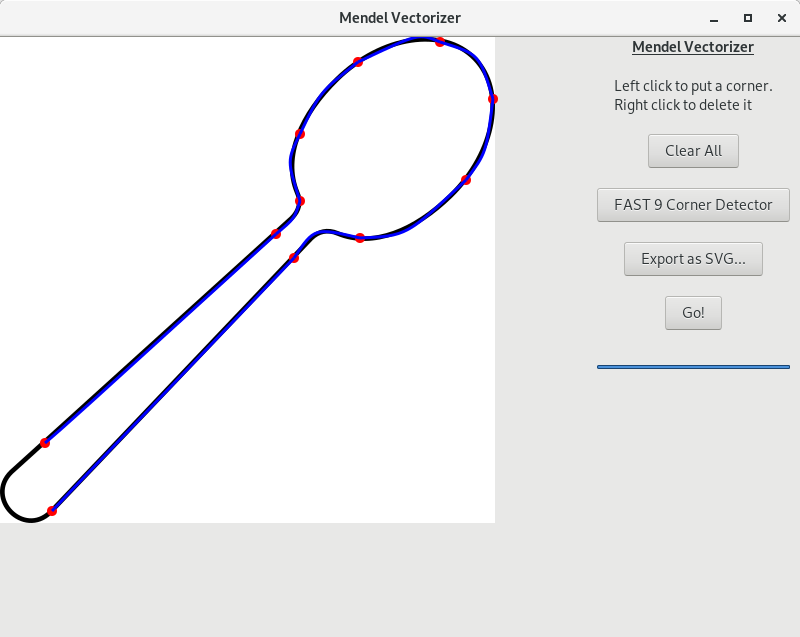
Existen varios algoritmos de búsqueda de esquinas: Harris, FAST9, FAST12, ... No obstante, no tuve muy buenos resultados en las imágenes con las que trabajaba. Así que esta parte del algoritmo se la dejo al humano. El humano se encargará de poner los puntos, en orden, que tiene que tratar de unir el algoritmo con curvas de Bézier.
Función de evaluación
Muchas veces la función de evaluación es el punto más delicado de estos algoritmos. En este caso la idea fundamental es identificar si la curva de Bézier está encima de la curva original. Para ello tomamos 100 puntos equidistantes de la curva de Bézier (con la ecuación paramétrica de la curva es muy sencillo).
[latex]\mathbf{B}(t)=\mathbf{P}_0(1-t)^3+3\mathbf{P}_1t(1-t)^2+3\mathbf{P}_2t^2(1-t)+\mathbf{P}_3t^3 \mbox{ , } t \in [0,1].[/latex]
Estos puntos se comparan con la imagen real, si ahí en la imagen original había una línea no pasa nada, si no, se resta 100. De este modo se penaliza gravemente salirse de la curva. Esto se hace así ya que la otra opción evidente (bonificar el estar sobre en la línea) podría dar lugar a resultados inesperados.
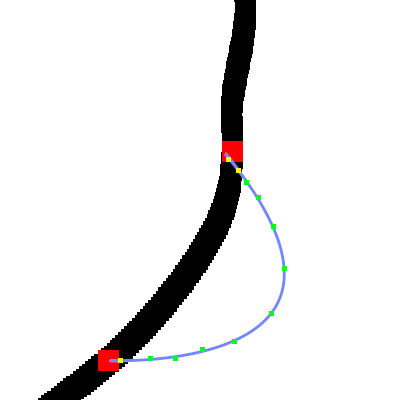
Pongamos como ejemplo una función de evaluación que bonifique por estar sobre la línea y no penalice por salirse de esta. Una línea bien adaptada a estas condiciones podría recorrerse toda la imagen, cruzando todas las líneas posibles, generando un garabato totalmente inútil pero muy bueno según esta función. Por ello, nuestra función de evaluación se basa en penalizar las salidas de la línea.
La función de evaluación presentada no es perfecta, ya que puede pasar de largo el punto final y dar la vuelta. Esta curva es más larga que la óptima, pero al estar completamente dentro de la línea negra original, la función de evaluación no la puede clasificar como peor que otras alternativas. Para solventar este problema una idea es que la longitud de la curva tenga una implicación en la función. No obstante, el cálculo de la longitud de una curva de Bezier es demasiado complejo y no lo he codificado. También podría aproximarse a través de segmentos rectos entre los 100 puntos calculados anteriormente.

pub fn evaluate(image: &GrayImage, line: &Bezier) -> f64 {
let mut eval = 0.0;
for point in line.iter() {
let x = point.x as u32;
let y = point.y as u32;
if image.in_bounds(x, y) {
let pixel = image.get_pixel(x, y);
if pixel.data[0] < 200 {
eval += 1.0;
} else {
eval -= 100.0;
}
} else {
eval -= 100.0;
}
}
eval
}Selección natural
La función de selección natural deja únicamente las 500 mejores curvas, de acuerdo a la función de evaluación, es decir, las mejor adaptadas de momento. Para la ordenación, Rust usa un algoritmo denominado Timsort, con coste O(nlogn). Sin embargo, en todo el algoritmo trabajamos con poblciones finitas, por lo que puede asimilarse a una constante, con coste O(1).
pub fn natural_selection(image: &GrayImage, mut population: Vec) -> Vec {
population.sort_by(|a, b| {
let a = evaluate(&image, &a);
let b = evaluate(&image, &b);
b.partial_cmp(&a).unwrap()
});
population.into_iter().take(GOOD_ONES).collect()
}Población inicial
La población inicial se forma con 1000 curvas generadas con parámetros totalmente aleatorios. Los valores de cada coordenada, eso sí, están comprendidos entre -d y d siendo d la distancia en línea recta entre los puntos de inicio y final.
let mut population = Vec::new();
let mut rng = thread_rng();
let distancia = start.distance(&end);
for _ in 0..1000 {
let xrand: f64 = rng.gen_range(-distancia, distancia);
let yrand: f64 = rng.gen_range(-distancia, distancia);
let mut control1 = start.middle(&end);
control1.x += xrand;
control1.y += yrand;
let mut control2 = start.middle(&end);
control2.x += xrand;
control2.y += yrand;
population.push(Bezier {
start,
end,
control1,
control2,
});
}Recombinado
El proceso de recombinación permite mezclar los mejores especímenes tratando de conseguir uno mejor. Este algoritmo genético es de tipo RCGA (Real Coded Genetic Algorithm) ya que los genes son números reales, en contraposición a los típicos genes binarios.Para estos algoritmos existen distintas variantes, aquí se usa el sistema de blend. El sistema de blend implica que de entre los dos padres se toman los valores mínimos y máximos para cada coordenada. Posteriormente se elige un nuevo valor de forma aleatoria con la condición de que esté dentro del rango de mínimo y máximo definido anteriormente.
// CROSSOVER
// Blend o Linear (Blend) https://engineering.purdue.edu/~sudhoff/ee630/Lecture04.pdf
let mut i: usize = 0;
let mut babies = Vec::new();
while i < GOOD_ONES {
let line1 = &population[i];
let line2 = &population[i + 1];
let min_x = line1.control1.x.min(line2.control1.x);
let max_x = line1.control1.x.max(line2.control1.x);
let min_y = line1.control1.y.min(line2.control1.y);
let max_y = line1.control1.y.max(line2.control1.y);
let control1 = Point {
x: rng.gen_range(min_x, max_x),
y: rng.gen_range(min_y, max_y),
};
let min_x = line1.control2.x.min(line2.control2.x);
let max_x = line1.control2.x.max(line2.control2.x);
let min_y = line1.control2.y.min(line2.control2.y);
let max_y = line1.control2.y.max(line2.control2.y);
let control2 = Point {
x: rng.gen_range(min_x, max_x),
y: rng.gen_range(min_y, max_y),
};
babies.push(Bezier {
start,
end,
control1,
control2,
});
i += 2;
}
population.append(&mut babies);Mutación
La fase de mutación permite generar pequeñas variaciones aleatorias respecto a la población. Afecta al 10% de la población aunque solo afecta a una coordenada a la vez.
Al ser un algoritmo RCGA, no vale simplemente con cambiar el valor de un bit. El enfoque utilizado en este algoritmo es el de una distribución normal de cambios de media 0. La distribución tiene la forma N(0,d/2). Esto implica que en la mayoría de las ocasiones la variación (tanto positiva como negativa) en la coordenada será bastante pequeña.

population = population
.into_iter()
.map(|mut line| {
if rng.gen::() < 0.10 {
let normal = Normal::new(0.0, distancia / 2.0);
let mutation_where: u32 = rng.gen_range(1, 5);
// Solo muta un gen, respecto a una Normal
match mutation_where {
1 => line.control1.x += rng.sample(normal),
2 => line.control1.y += rng.sample(normal),
3 => line.control2.x += rng.sample(normal),
4 => line.control2.y += rng.sample(normal),
_ => (),
}
}
line
})
.collect();El programa: Mendel Vectorizer
El programa definitivo, Mendel Vectorizer, disponible en GitHub, tiene más detalles. La interfaz gráfica está hecha usando GTK, la interfaz de línea de comandos usa Clap y el algoritmo se ejecuta en paralelo usando paso de mensajes entre los hilos. El programa genera un fichero SVG resultado que puede ser abierto en programas como Inkscape o Adobe Illustrator.
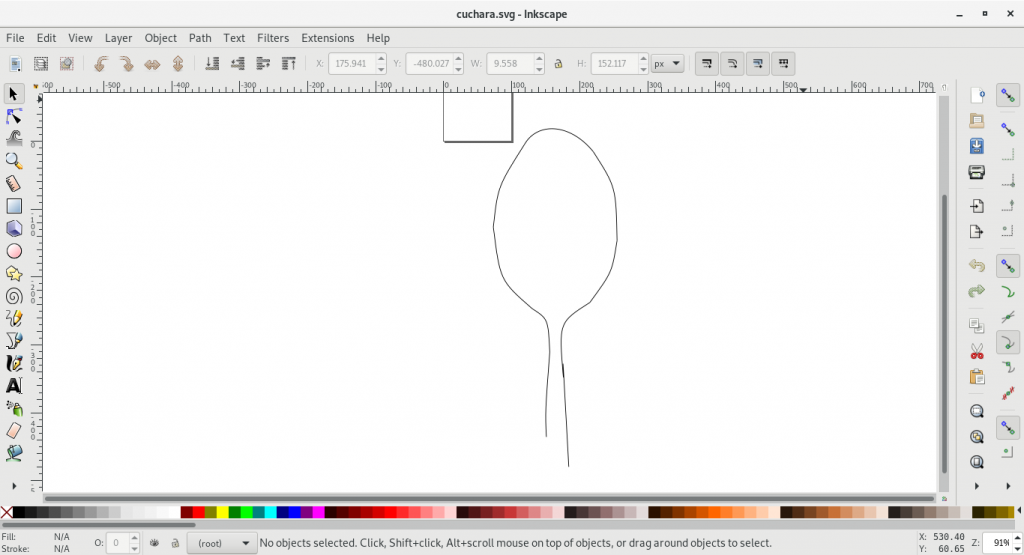
Para usar Mendel Vectorizer en tu ordenador, sigue los siguientes pasos.
Descárgate una copia del código con Git. Compila con Rust (una edición que soporte la edición 2018, mínimo la 1.31) y ejecútalo.
git clone https://github.com/aarroyoc/mendel-vectorizercd mendel-vectorizercargo buildcargo runTambién podéis descargaros la memoria en PDF del programa.