El Algoritmo Simplex
El algoritmo Simplex es el método más conocido para resolver problemas de programación lineal. Diseñado en 1947 por George Dantzig, nos ofrece una forma eficiente y genérica de resolver este tipo de problemas, de gran utilidad en la industria. Se trata de uno de los diez algoritmos más importantes del siglo XX, según IEEE y el American Institute of Physics.
En este post vamos a explicar el algoritmo Simplex. Al final, encontraréis el código de la versión en Rust. Quería comentar el código directamente, pero creo que es un algoritmo demasiado complejo como para entenderlo directamente.
¿Qué es la programación lineal?
La programación lineal es un método para obtener el mejor resultado posible dado un modelo matemático que usa relaciones lineales. Un ejemplo de programación lineal sería, ¿cómo hay que distribuir las antenas de móvil para tener una cobertura completa gastando el menor dinero posible? Como este hay miles de problemas que pueden modelarse con programación lineal. Si quieres saber más sobre esto, hace tiempo hice una entrada explicando qué es la programación lineal más en detalle.
Elaboración de la tabla
El algoritmo Simplex se compone de dos etapas: encontrar una solución factible y después, mejorarla. Con solución factible nos referimos a una solución que cumpliría todas las ecuaciones que vamos a añadir pero que no tiene por qué ser óptima. Una vez tengamos eso, vamos a mejorar la solución hasta que ya no sea posible y siempre transitando entre soluciones factibles, pero mejores.
El algoritmo se basa en la existencia de una tabla, anotada en los extremos. En la primera fila tendremos un 1 seguido del renglón Z y el valor óptimo.
Las siguientes filas representan a las restricciones. Tienen anotada a la izquierda una variable, en el centro las restricciones en sí y en la última columna el valor de esa variable que hace óptimo el resultado.
En esta tabla puedes ver de forma esquemática la tabla:
| 1 | Renglón Z | Valor Óptimo |
| Base | Restricciones | Valor Variable |
El renglón Z se forma con la función objetivo cambiada de signo. El valor óptimo comienza en cero. Las restricciones no tienen modificaciones y el valor de variable inicial es el valor al otro lado de la ecuación de la restricción. Lo más complicado es la elección de variables de la base. Tiene que formar una solución factible desde el principio. Manualmente pueden hacerse muchas cosas, pero de forma automatizada es más complejo.
Una forma fácil de encontrar una solución factible inicial es traducir las inecuaciones mayor o igual que y menor o igual que en igualdades, añadiendo variables de holgura (o slack). Esto en muchos casos podría ser suficiente, pero para asegurarnos, podemos introducir variables artificiales.
El problema de añadir variables artificiales es que los resultados pueden ser falsos, ya que amplían el "número de soluciones". Existen varias formas de añadir variables artificiales sin dar respuestas falsas. Una es el método de la doble fase, que consiste en realizar dos tablas Simplex. Otra solución es el método de la gran M, que consiste en penalizar fuertemente las variables artificiales, para que nunca puedan entrar a la base.
Veamos un ejemplo real:
minimize -3x + y - 2z
with 2x - 2y + 3z <= 5
x + y - z <= 3
x - y + z <= 2
La tabla correspondiente sería la siguiente:
| z | x1 | x2 | x3 | x4 | x5 | x6 | LD | |
| z | 1 | 3 | -1 | 2 | 0 | 0 | 0 | 0 |
| x4 | 0 | 2 | -2 | 3 | 1 | 0 | 0 | 5 |
| x5 | 0 | 1 | 1 | -1 | 0 | 1 | 0 | 3 |
| x6 | 0 | 1 | -1 | 1 | 0 | 0 | 1 | 2 |
En este ejemplo, hemos creado 3 variables de slack, para convertir los menor o igual en igual. Estas variables de slack hacen la matriz identidad en su parte de las restricciones, por lo que pueden entrar a la base. Ahora bien, estas variables no aparecen en la función objetivo, así que las marcamos a cero en el renglón Z. Con variables artificiales, se haría todo igual, salvo que en vez de cero, se debe poner un M muy muy grande.
Pivotando
El segundo paso es mejorar la solución hasta llegar al óptimo. ¿Cuándo tenemos un óptimo? Cuando todo el renglón Z sea menor o igual a cero. Si además, todos los elementos de Z restados de su valor en la función objetivo son estrictamente menores que cero, la solución es única.
Nuestro objetivo, por tanto, es conseguir valores negativos en el renglón Z.
Para ello vamos a introducir una variable en la base (que no estuviese ya) y vamos a sacar una. La variable de entrada puede ser cualquiera en cuyo renglón Z sea positiva.
En nuestro caso concreto, vamos a elegir introducir x1, cuyo renglón Z es 3.
La variable de salida es aquella que en la columna de la variable de entrada es positiva y tiene el valor más pequeño en la división de la columna LD por el propio valor. Si no se encuentran valores positivos, el problema no tiene límite y la solución es infinita.
En nuestro ejemplo, tendríamos que calcular para x4=5/2, para x5=3/1 y para x6=2/1. El valor más pequeño el de x6, así que x6 sale de la base.
Ese punto, marcado con negrita, va a ser el pivote.
| z | x1 | x2 | x3 | x4 | x5 | x6 | LD | |
| z | 1 | 3 | -1 | 2 | 0 | 0 | 0 | 0 |
| x4 | 0 | 2 | -2 | 3 | 1 | 0 | 0 | 5 |
| x5 | 0 | 1 | 1 | -1 | 0 | 1 | 0 | 3 |
| x6 | 0 | 1 | -1 | 1 | 0 | 0 | 1 | 2 |
Se pivota de la siguiente forma:
La fila del pivote se tiene que dividir entre el valor del pivote (en este caso hay que dividir entre 1, se queda todo igual). Después se va fila por fila restándolas el valor de la fila del pivote por el elemento de la misma columna de esa fila que el pivote. Es decir, en la primera fila, la del renglón Z, hay que restar la fila de x6 multiplicada por 3. Debería quedarnos al finalizar una columna con todo ceros, salvo el pivote.
El resultado final es el siguiente:
| z | x1 | x2 | x3 | x4 | x5 | x6 | LD | |
| z | 1 | 0 | 2 | -1 | 0 | 0 | -3 | -6 |
| x4 | 0 | 0 | 0 | 1 | 1 | 0 | -2 | 1 |
| x5 | 0 | 0 | 2 | -2 | 0 | 1 | -1 | 1 |
| x1 | 0 | 1 | -1 | 1 | 0 | 0 | 1 | 2 |
Ahora debería entrar la variable x2 y saldría x5.
| z | x1 | x2 | x3 | x4 | x5 | x6 | LD | |
| z | 1 | 0 | 0 | 1 | 0 | -1 | 2 | -7 |
| x4 | 0 | 0 | 0 | 1 | 1 | 0 | -2 | 1 |
| x2 | 0 | 0 | 1 | -1 | 0 | 0.5 | -0.5 | 0.5 |
| x1 | 0 | 1 | 0 | 0 | 0 | 0.5 | 0.5 | 2.5 |
Por último, debe entrar x3 y salir x4.
| z | x1 | x2 | x3 | x4 | x5 | x6 | LD | |
| z | 1 | 0 | 0 | 0 | -1 | -1 | 0 | -8 |
| x3 | 0 | 0 | 0 | 1 | 1 | 0 | -2 | 1 |
| x2 | 0 | 0 | 1 | 0 | 1 | 0.5 | -2.5 | 1.5 |
| x1 | 0 | 1 | 0 | 0 | 0 | 0.5 | 0.5 | 2.5 |
En este punto ya hemos alcanzado el óptimo, -8, aunque no es la única solución posible que da este valor. La solución del problema es x1=2.5, x2=1.5 y x3=1.
Resolviendo con la librería simplex de Rust
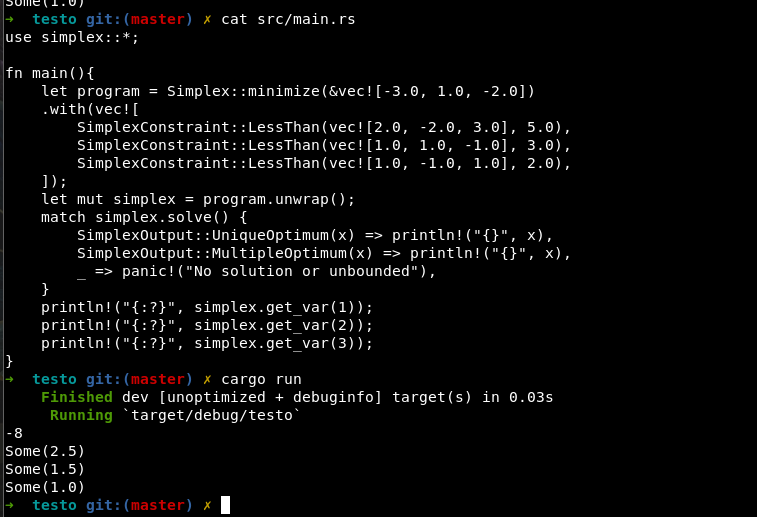
Estas mismas operaciones (y alguna más) son las que realiza por debajo la librería simplex, disponible para Rust. He intentado que la librería sea lo más sencilla de usar. Con el siguiente código se resuelve el mismo problema:
use simplex::*;
fn main(){
let program = Simplex::minimize(&vec![-3.0, 1.0, -2.0])
.with(vec![
SimplexConstraint::LessThan(vec![2.0, -2.0, 3.0], 5.0),
SimplexConstraint::LessThan(vec![1.0, 1.0, -1.0], 3.0),
SimplexConstraint::LessThan(vec![1.0, -1.0, 1.0], 2.0),
]);
let mut simplex = program.unwrap();
match simplex.solve() {
SimplexOutput::UniqueOptimum(x) => println!("{}", x),
SimplexOutput::MultipleOptimum(x) => println!("{}", x),
_ => panic!("No solution or unbounded"),
}
println!("{:?}", simplex.get_var(1));
println!("{:?}", simplex.get_var(2));
println!("{:?}", simplex.get_var(3));
}
Existe un algoritmo similar llamado Revised Simplex. Este ocupa menos memoria y las implementaciones más potentes como CPLEX o Xpress se suelen basar en él. Échale un ojo si te interesa.