Triángulo de Sierpinski en JavaScript
- Adrián Arroyo Calle
Un amigo me propuso esta mañana que viera un vídeo de Numberphile, concretamente uno titulado Chaos Game. El vídeo es bastante interesante y habla de como de una aparente aleatoriedad es posible sacar fractales y patrones regulares. Esta misma mañana al llegar a casa y antes de comer me he picado y me he puesto a implementar el algoritmo en JavaScript usando el Canvas de HTML5. El resultado lo tenéis aquí:
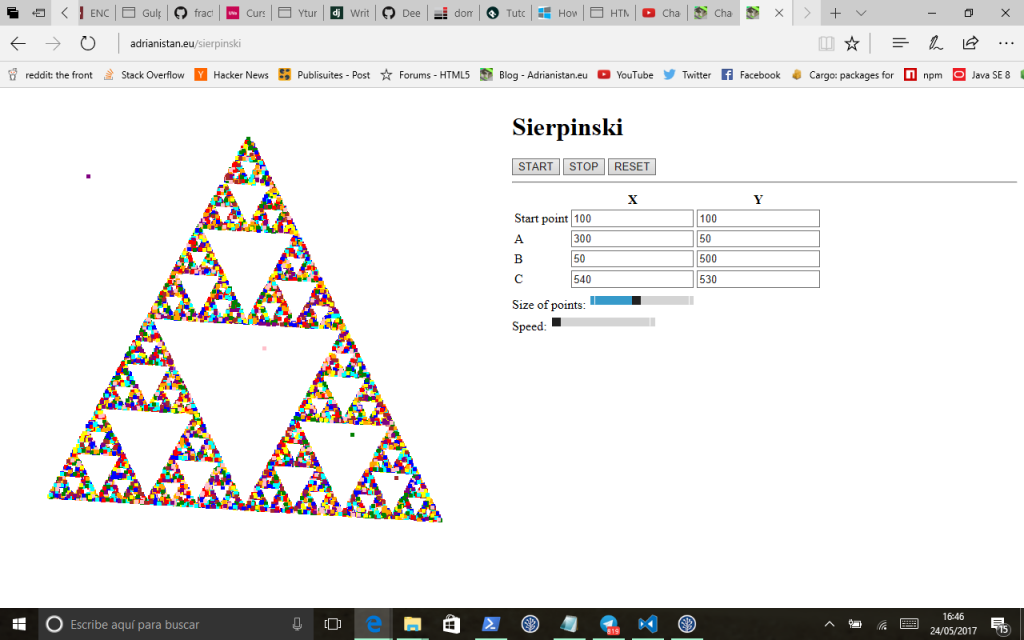
Y el código que lleva es el siguiente:
Con distinto número de vértices existen otros fractales, también muy chulos. Incluso en el vídeo de Numberphile realizan un fractal con un gran parecido a una hoja de helecho, usando dos triángulos y una ligera modificación del algoritmo.
Un saludo y soñad con fractales.

http://adrianistan.eu/sierpinski/
Y el código que lleva es el siguiente:
const COLOR_LIST = ["red","green","yellow","pink","brown","purple","cyan","blue","orange"];
function punto(x,y){
var p = {
x:x,
y:y
};
return p;
}
function puntoMedio(p,q){
var m = {
x: Math.round((p.x+q.x)/2),
y: Math.round((p.y+q.y)/2)
};
return m;
}
function getRandomColor(){
return COLOR_LIST[Math.floor(COLOR_LIST.length * Math.random())];
}
function dibujarPunto(ctx,p,size){
ctx.fillStyle = getRandomColor();
ctx.fillRect(p.x,p.y,size,size);
}
function $(id){
return document.getElementById(id);
}
function get(id){
return Math.round(document.getElementById(id).value);
}
function main(){
var canvas = document.getElementById("canvas");
var ctx = canvas.getContext("2d");
var interval;
$("start").addEventListener("click",function(){
var size = get("size");
var vertex = [punto(get("a-x"),get("a-y")),punto(get("b-x"),get("b-y")),punto(get("c-x"),get("c-y"))];
let p = punto(get("s-x"),get("s-y"));
dibujarPunto(ctx,p,size);
interval = setInterval(function(){
var q = vertex[Math.floor(3*Math.random())];
p = puntoMedio(p,q);
dibujarPunto(ctx,p,size);
},get("speed"));
});
$("stop").addEventListener("click",function(){
clearInterval(interval);
});
$("reset").addEventListener("click",function(){
ctx.fillStyle = "white";
ctx.fillRect(0,0,600,600);
});
}
window.addEventListener("DOMContentLoaded",main);
Con distinto número de vértices existen otros fractales, también muy chulos. Incluso en el vídeo de Numberphile realizan un fractal con un gran parecido a una hoja de helecho, usando dos triángulos y una ligera modificación del algoritmo.
Un saludo y soñad con fractales.
Comentarios