Hace ya bastante tiempo quese viene hablando de ordenadores cuánticos. ¿Qué son? ¿En qué se diferencian de los ordenadores clásicos? ¿Son de verdad tan potente como dicen?

En este largo artículo, ideal para el verano, vamos a ver los principios fundamentales de los ordenadores cuánticos más allá de lo que la típica revista o web te podría contar. Veremos qué es un qubit y algunas puertas lógicas interesantes, así como su aplicación.

Los ordenadores cuánticos actuales requieren temperaturas de funcionamiento cercanas al cero absoluto

Notación de Dirac

Lo primero antes de entrar en materia cuántica, será adaptar nuestra notación clásica, a otra más potente. Esta notación que vamos a ver, llamada notación de Dirac o Bra-ket, nos será muy útil ya que los bits clásicos no son más que un caso concreto de qubit en esta notación.

En esta notación tenemos que representar los bits como matrices. Un conjunto de N bits se representa con una matriz de 1 columna y [latex]2^N[/latex] filas. En todas las posiciones existen ceros salvo para la posición que representa la combinación que representa. Veamos algunos ejemplos sencillos:

Un bit con valor 0 se representa así

[latex]
| 0 \rangle = \begin{pmatrix}
1\\
0
\end{pmatrix}[/latex]

Un bit con valor 1 se representa así:

[latex]
| 1 \rangle = \begin{pmatrix}
0\\
1
\end{pmatrix}[/latex]

Aquí contamos como en informática, empezando desde cero. Como ves la posición 0 del vector solo es 1 cuando representa el bit 0. Si la posición que tiene el 1 es la segunda, representa el bit 1.

La parte que va a la izquierda del igual se llama ket. En este caso hemos representado ket 0 y ket 1.

Si tenemos más bits se puede hacer de la misma forma. Vamos a representtar ket 10. 10 en binario es 2, así que estará en la posición tercera.

[latex]
| 10 \rangle = \begin{pmatrix}
0\\
0\\
1\\
0
\end{pmatrix}[/latex]

Puertas lógicas como producto de matrices

¿Recuerdas el producto de matrices de tus clases de álgebra? Resulta que todas las puertas lógicas clásicas pueden representarse como producto de matrices. Por ejemplo, la puerta lógica NOT se puede implementar con esta matriz:

[latex]
\begin{pmatrix}
0 & 1 \\
1 & 0 \\
\end{pmatrix}
[/latex]

Y aquí la vemos en acción

[latex]
\begin{pmatrix}
0 & 1 \\
1 & 0 \\
\end{pmatrix}\begin{pmatrix}
1 \\
0
\end{pmatrix}
=
\begin{pmatrix}
0 \\
1
\end{pmatrix}
[/latex]

También podría hacerse con la puerta AND que toma como entrada dos bits.

[latex]
\begin{pmatrix}
1 & 1 & 1 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
0 \\
0 \\
0 \\
1
\end{pmatrix}
=
\begin{pmatrix}
0 \\
1
\end{pmatrix}
[/latex]

Un teclado con puertas cuánticas

Juntando bits

Para formar bits más grandes ya sabemos que tenemos que tener una matriz tan grande como combinaciones haya ([latex]2^N[/latex] posiciones, N bits). Existe una forma de calcular automáticamente la posición que hay que marcar y es hacer el producto tensorial. Si no sabes calcularlo no importa mucho, porque apenas lo vamos a usar, pero puedes ver un ejemplo de como funciona. En este ejemplo, queremos juntar los bits 1 y 1 (3 en decimal).

[latex]
\begin{pmatrix}
0 \\
1
\end{pmatrix}
\otimes
\begin{pmatrix}
0 \\
1
\end{pmatrix}
=
\begin{pmatrix}
0 \\
0 \\
0 \\
1
\end{pmatrix}
[/latex]

Qubits

Hasta ahora no hemos visto nada realmente nuevo, solo hemos preparado el terreno para dejar paso a los qubits. Personalmente desconocía que podían usarse matrices para operar con bits y aunque no es tan práctico como otros sistemas, lo cierto es que es muy explícito y elegante.

Los qubits son bits como los que hemos visto antes pero tienen un estado indeterminado. No es que tengan un valor de forma secreta y no sepamos cuál es. Podríamos decir que son los dos valores clásicos a la vez, como el gato de Schrodinger. Cuando realizamos una observación sobre el qubit, este colapsa y podemos ver uno de los dos estados. ¿Cuál vemos? No podemos saberlo a priori, pero hay probabilidades. Los bits clásicos no son más que qubits cuyas probabilidades de colapsar a 0 o 1 es del 100%, por tanto no hay duda y su valor sí que está determinado.

¿Cómo representamos los qubits y sus estados cuánticos? Con números complejos. Si recuerdas, estos eran los que tenían una parte real y una imaginaria. No obstante, voy a tomar solo los números reales para simplificar. Los números reales son números complejos válidos, pero los complejos son mucho más extensos.

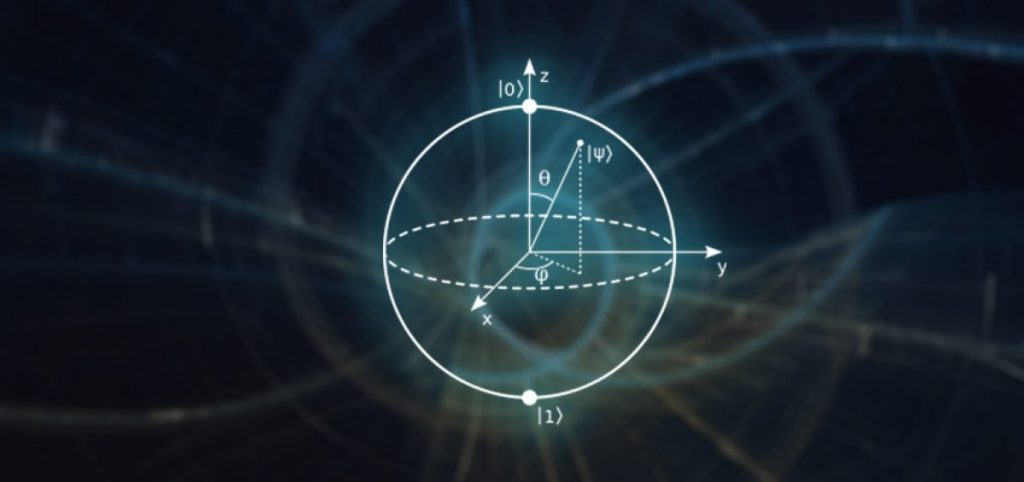La esfera de Bloch permite representar todos los estados cuánticos (números complejos)

Para calcular la probabilidad que tiene un estado cuántico de colapsar a un valor, hacemos el módulo y elevamos al cuadrado: [latex]|a|^2[/latex].

Todo qubit además debe cumplir una propiedad fundamental:

[latex]
\begin{pmatrix}
a \\
b
\end{pmatrix}
\text{ es un qubit}
\Leftrightarrow
|a|^2 + |b|^2 = 1
[/latex]

Y es que la probabilidad de ser 0 y de ser 1 sumadas deben equivaler al suceso seguro, es decir, 1. 100% de probabilidades de que de 0 o 1.

Con esto ya podemos definir algunos qubits.

[latex]
\begin{pmatrix}
\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}}
\end{pmatrix}
[/latex]

Este es mi qubit preferido. Representa el estado de superposición cuántica. Cada valor tiene el 50% de probabilidades de salir. [latex]|\frac{1}{\sqrt{2}}|^2 = \frac{1}{2}[/latex]. Cuando colapsemos el qubit al observarlo será como lanzar una moneda al aire.

Otro detalle que a veces se nos pasa por alto es que los qubits pueden contener valores negativos. Estos qubits son físicamente diferentes a los positivos, pero tienen las mismas probabilidades de colapsar en los mismos valores que los positivos.

[latex]
\begin{pmatrix}
-1 \\
0
\end{pmatrix}
[/latex]

Es un qubit válido, que colapsa con 100% de probilidad a 0.

¿Cómo se representan los qubits en notación de Dirac? Representando la probabilidad que tiene cada combinación de bits de aparecer. Para un qubit sería algo así:

[latex]
\alpha | 0 \rangle + \beta | 1 \rangle
[/latex]

Siendo [latex]\alpha[/latex] y [latex]\beta[/latex] las probabilidades de colapsar a cada estado.

Puertas cuánticas

Ahora vamos a ver cuáles son las puertas lógicas más importantes del mundo cuántico.

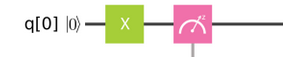
Negación (Pauli X)

Esta es exactamente igual que en el mundo clásico, con la misma matriz que hemos visto antes. Su símbolo es el cuadrado con una X.

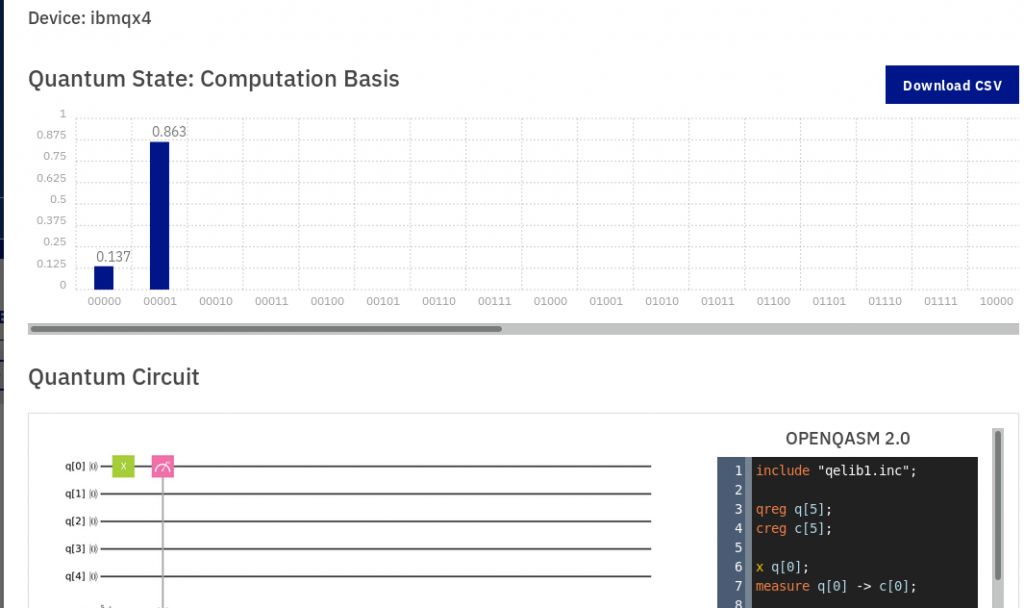
Aquí vemos una imagen del simulador IBM Q usando la puerta X cuántica. IBM nos deja ejecutarlo en ordenadores cuánticos reales. Veamos los resultados.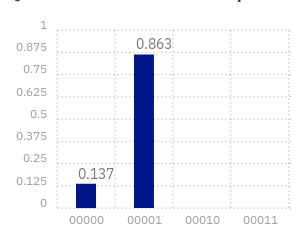

¡Terrible! La mayoría de casos, el ordenador cuántico responde 1, el valor correcto, pero un 13% de los casos no. Teóricamente había una probabilidad del 100% y en la práctica solo es del 86.3%. ¡Y solo es una puerta X! Es por ello que los procesadores cuánticos todavía necesitan mejorar mucho. Google, Microsoft e IBM están investigando de forma independiente en ordenadores cuánticos. Veremos quién consigue tener antes ordenadores cuánticos precisos (aunque hay expertos que piensan que nunca se podrá lograr).

CNOT

Esta puerta es muy interesante. Toma dos qubits, uno de control, que permanece invariable al traspasar la puerta y otro de datos. Al qubit de datos se le aplica la puerta X si el qubit de control está activo. Su matriz es la siguiente:

[latex]
CNOT = \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{pmatrix}
[/latex]

Se reprensenta de esta forma:

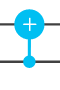O similar, porque los símbolos de computación cuántica no están todavía muy estandarizados. El punto grande es el qubit de control y el punto pequeño está sobre el qubit de datos.

HADAMARD

Esta puerta es quizá la más famosa del mundo cuántico. Veamos su matriz:

[latex]
\begin{pmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{pmatrix}
[/latex]

Esta puerta permite poner un qubit clásico en estado de superposición cuántica. Y también deshacerlo. Es muy usada en algoritmos cuánticos. Se representa con un cuadrado y una H.

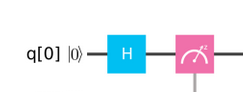Los resultados en el ordenador cuántico real de IBM Q son:

Cuando debería de ser bastante más cercano a 50% en los dos valores.

Con esto ya tenemos las puertas más usadas. Básicamente con Hadamard, X y CNOT se pueden implementar casi todos los circuitos cuánticos. Solo nos faltarían las puertas que operan entran en números complejos para poder implementar todos los circuitos.

Algoritmo de Deutsch-Jozsa

El algoritmo de Deutsch-Jozsa es uno de los algoritmos cuánticos más sencillos de entender y que mejoran drásticamente el rendimiento respecto a un algoritmo clásico.

El planteamiento básico es que tenemos una caja negra que aplica una función sobre un bit. Estas funciones pueden ser: set-to-0, set-to-1 (ambas constantes), identidad (no cambiar nada) y X (ambas dinámicas) . Si queremos saber que función contiene la caja negra, ¿Cuántas veces tenemos que pasar valores? En una CPU clásica tendríamos que hacerlo dos veces para poder determinar que función contiene la caja negra. En una CPU cuántica... también. No hay diferencia. Pero, si cambiamos la pregunta a ¿de qué categoría es la función de la caja negra?, la cosa cambia. En una CPU clásica seguiríamos necesitando 2 pruebas, pero en una CPU cuántica y con un circuito por el exterior, podemos aprovechar la superposición cuántica para realizar una sola prueba y determinar si en el interior hay una función constante o dinámica.

Vamos a ver estas 4 funciones de la caja negra como son:

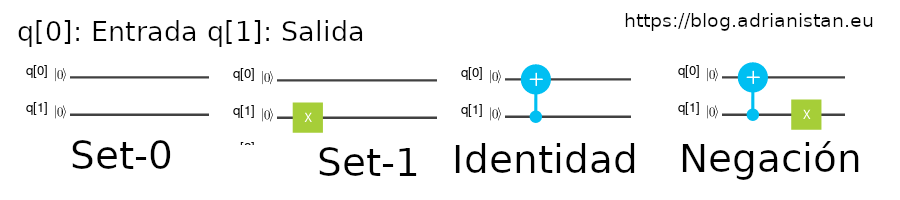¿Se te ocurre como puedes crear un circuito fuera de la caja negra que con una sola prueba, ya sepa si estamos ante las funciones Set-0, Set-1 o Identidad, Negación?

El circuito es el siguiente:

Tal y como está diseñado si en q[1] medimos 0, la función es de tipo constante y si medimos 1, es de tipo dinámica. Un desarrollo matemático de los productos de matrices, como el que hay en Wikipedia, te mostrará como siempre es cierto. Este también es un ejemplo de como los ordenadores cuánticos pueden dar resultados totalmente deterministas.

Esta idea, se puede generalizar y extrapolar a otros problemas, generando una colección muy interesante de algoritmos que se ejecutan en tiempo exponencialmente menor que en una CPU clásica.

Algoritmos de Shor y de Grover

Estos dos algoritmos han sido llamados los killer apps de la computación cuántica, ya que son algoritmos que mejoran sustancialmente (uno de forma exponencial, otro de forma cuadrática) los tiempos de problemas reales.

El algoritmo de Shor fue el primero en ser descubierto, en 1994 por Peter Shor. Sirve para factorizar números (es decir, sacar los números primos que multiplicados generan el número original). Lo puede hacer en [latex]O((\log{n})^3)[/latex]. De este modo, los algoritmos tipo RSA que se basan en la factorización de números podrían romperse en tiempo polinómico, por lo cuál RSA ya no serviría como protección. El algoritmo de Shor no da siempre los resultados correctos, pero tiene una probabilidad de éxito superior a la de fracaso, por lo que con repetir múltiples veces la ejecución podríamos estar casi seguros del resultado.

El algoritmo de Grover fue descubierto en 1996 por Lov Grover y permite buscar en una lista no ordenada de datos en [latex]O(\sqrt{n})[/latex] mientras que en una computadora clásica sería [latex]O(n)[/latex].

Estos dos algoritmos sin duda marcan lo que se ha llamada la supremacía cuántica y que ocurrirá cuando los ordenadores cuánticos puedan ejecutar con suficiente precisión estos algoritmos y su utilidad en el mundo real supere a la de los algoritmos clásicos.

Entrelazamiento cuántico

Ya hemos visto las bases de los circuitos cuánticos. Ahora veamos algunas consecuencias de todo lo anterior. Cosas cuánticas que parecen hasta cierto punto fuera de la lógica. ¿Qué ocurre si tenemos varios qubits en un estado como este?

[latex]
\begin{pmatrix}
\frac{1}{\sqrt{2}} \\
0 \\
0 \\
\frac{1}{\sqrt{2}}
\end{pmatrix}
[/latex]

En este estado solo puede colapsar a 00 o a 11. ¿Esto qué significa? Significa que los qubits están entrelazados entre sí, uno depende de otro, si los separamos y uno colapsa a 0, el otro colapsa a 0. Si uno colapsa a 1, el otro colapsa a 1.

Es importante destacar que los qubits pueden separarse en este estados. Los qubits alejados a millones de kilómetros siguen entrelazados y el valor al que deciden colapsar se decide de forma instantánea. Esto quiere decir que se sincronizan a una velocidad superior a la de la luz. El truco es que no se transmite información, por eso el universo lo permite, pero esto permite realizar la teletransportación cuántica.

La forma de entrelazar qubits es muy sencilla, con una puerta Hadamard y una CNOT.

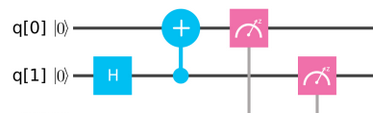
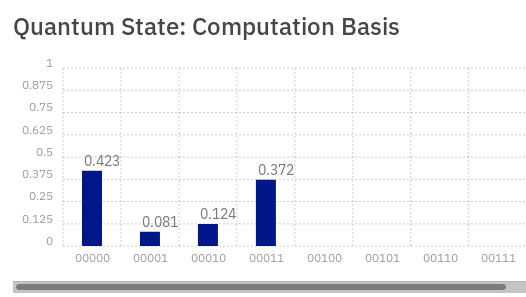IBM Q todavía tiene que mejorar, pero se aprecia claramente el entrelazamiento cuántico.

Teletransportación cuántica

La teletransportación existe, al menos entre qubits. Y es instantánea (más o menos). La teletransportación cuántica la podemos provocar usando varios qubits entrelazados. Necesitamos 3 qubits. El qubit que va a ser teletransportado, un qubit del emisor y un qubit del receptor. La idea es entrelazar el emisor con el receptor (qubit de destino) y posteriormente el qubit del emisor con el qubit que va a ser transportado.

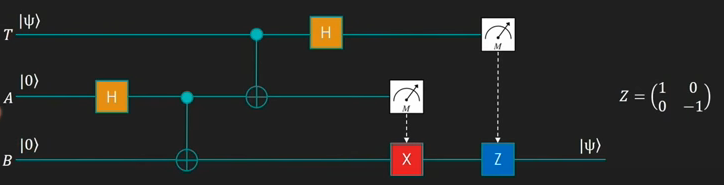No he sido capaz de hacer que IBM Q haga una teletransportación, así que aquí viene un esquema distinto. T es el qubit a transportar, A es el emisor y B el receptor. En este ejemplo se usa la puerta Pauli Z, cuya matriz es la indicada.

El truco de la teletransportación instantánea tiene que ver con que A y B tienen que estar entrelazados, por tanto, han tenido que ser transportados a sus respectivos lugares anteriormente a velocidad inferior a la luz.

Esto teletransporta qubits pero no hace copias. Esto es debido al Teorema de No Clonación.

Lenguajes de programación

Mientras esperamos a que los ordenadores cuánticos sean lo suficientemente estables, ya existen lenguajes de programación que podemos usar en simuladores. Quizá el más conocido sea Q# de Microsoft (funciona en Linux, tranquilos), que guarda similitudes con C#. Otro bastante usado es OpenQasm de IBM, algo más parecido a ensamblador.

namespace Quantum.Bell
{
    open Microsoft.Quantum.Primitive;
    open Microsoft.Quantum.Canon;

    operation Set (desired: Result, q1: Qubit) : ()
    {
        body
        {
            let current = M(q1);
            if (desired != current)
            {
                X(q1);
            }
        }
    }
    operation BellTest (count : Int, initial: Result) : (Int,Int,Int)
    {
        body
        {
            mutable numOnes = 0;
            mutable agree = 0;
            using (qubits = Qubit[0])
            {
                for (test in 1..count)
                {
                    Set (initial, qubits[0]);
                    Set (Zero, qubits[1]);

                    H(qubits[0]);
                    CNOT(qubits[0],qubits[1]);
                    let res = M (qubits[0]);

                    if (M (qubits[1]) == res) 
                    {
                        set agree = agree + 1;
                    }

                    // Count the number of ones we saw:
                    if (res == One)
                    {
                        set numOnes = numOnes + 1;
                    }
                }

                Set(Zero, qubits[0]);
            }
            // Return number of times we saw a |0> and number of times we saw a |1>
            return (count-numOnes, numOnes, agree);
        }
    }
}

Este es un ejemplo de lanzar la moneda con entrelazamiento cuántico en Q#, el lenguaje cuántico de Microsoft.

Referencias

Quantum Computing for Computer Scientists
Cats, Qubits, and Teleportation: The Spooky World of Quantum Algorithms
Microsoft Quantum Development Kit: Introduction and step-by-step demo
Qubit